Find Axis Of Symmetry: Formula, Examples & Graphing - Math Help

25 May, 2025

Ever wondered what makes a parabola, that graceful U-shaped curve, so visually captivating? The secret lies in its axis of symmetry, a fundamental concept that underpins the very essence of this mathematical marvel.

Understanding the axis of symmetry is not merely an academic exercise; it unlocks a deeper comprehension of parabolas and their properties. This understanding transcends the classroom, offering insights into real-world applications, from the design of satellite dishes to the trajectory of a thrown ball. This exploration will delve into the methods for identifying and utilizing the axis of symmetry, equipping you with the tools to navigate the world of parabolas with confidence.

Here is a table that will help you understand the Axis of Symmetry:

Feature	Description
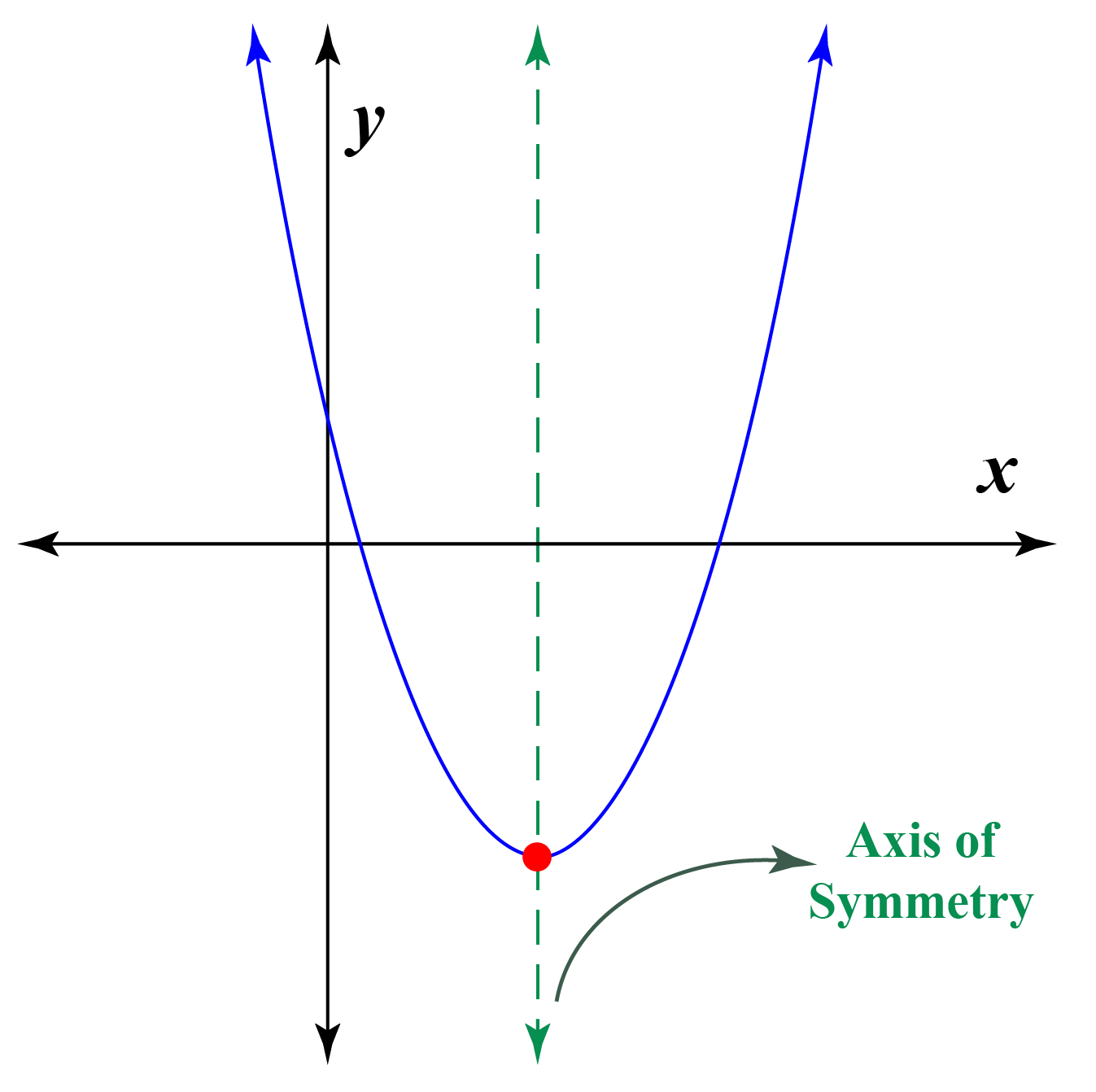
Definition	The axis of symmetry is a straight line that divides a parabola into two symmetrical halves.
Key Property	Every point on one side of the parabola has a corresponding point on the other side, equidistant from the axis of symmetry.
Location	It always passes through the vertex of the parabola.
Orientation	Can be vertical (for parabolas opening up or down) or horizontal (for parabolas opening left or right).
Significance	Provides a reference for the symmetry of the parabola, useful for finding the vertex, roots (x-intercepts), and understanding the behavior of the function.
Equation (Vertical Parabola)	For a quadratic function in the form f(x) = ax + bx + c, the axis of symmetry is given by the equation x = -b/2a.
Equation (Vertex Form)	If the equation is in vertex form, f(x) = a(x - h) + k, the axis of symmetry is x = h.

For further detailed information and real world examples, you can explore the following authentic website: Khan Academy - Axis of Symmetry.

To truly grasp the concept, lets examine the various forms in which a quadratic equation, the defining equation of a parabola, can appear and how to extract the axis of symmetry from each. The standard form, the vertex form, and the use of intercepts all provide unique avenues to this fundamental element.

Finding the Axis of Symmetry from the Standard Form

The standard form of a quadratic equation is often expressed as f(x) = ax + bx + c. The beauty of this form lies in the directness it offers to the process of finding the axis of symmetry. The formula x = -b/2a is the key. Armed with this formula, we can swiftly determine the vertical line that bisects the parabola.

Consider an example: f(x) = 2x + 8x + 3. Here, a = 2, b = 8, and c = 3. Applying the formula, x = -8/(2*2) = -2. Therefore, the axis of symmetry is the vertical line x = -2.

Unveiling the Axis of Symmetry with the Vertex Form

The vertex form, represented as f(x) = a(x - h) + k, is particularly insightful. This form reveals the vertex of the parabola directly, which is the point (h, k). Since the axis of symmetry passes through the vertex, the equation of the axis of symmetry is simply x = h. It's a straightforward deduction that bypasses complex calculations.

For instance, if the equation is f(x) = 3(x + 1) - 4, the vertex is (-1, -4). Consequently, the axis of symmetry is x = -1. This method showcases the utility of understanding different forms of the quadratic equation.

Using Roots or X-Intercepts to Discover Symmetry

Another method involves the x-intercepts, also known as the roots or zeros, of the parabola. These are the points where the parabola intersects the x-axis. If a parabola intersects the x-axis at two distinct points, the axis of symmetry lies exactly in the middle of these points. The x-coordinate of the vertex, and therefore the axis of symmetry, can be found by averaging the x-intercepts.

If the x-intercepts are x and x, the axis of symmetry is x = (x + x)/2. This method is beneficial when the roots are easily identifiable from a graph or by solving the quadratic equation. The symmetry inherent in parabolas provides a direct pathway to the axis of symmetry via its roots.

Visualizing Symmetry: The Role of the Graphing Calculator

In the modern age, technology offers indispensable tools for visualization. Graphing calculators and online graphing tools are invaluable for understanding the axis of symmetry. By inputting the equation of a parabola, one can instantly see the graph and the axis of symmetry. These tools not only verify calculations but also provide a dynamic and interactive way to explore the concept.

Plotting points, visualizing algebraic equations, adding sliders, and animating graphs are all within reach. This interactive approach transforms abstract concepts into tangible understanding, allowing for a deeper appreciation of the symmetrical nature of parabolas.

Symmetry in Action: Examples and Applications

The applications of understanding the axis of symmetry extend far beyond textbook problems. Consider the design of a satellite dish, where the parabolic shape reflects signals to a central focus point. The axis of symmetry determines the precise orientation and placement of the dish, ensuring optimal signal reception. The same principle applies to the headlights of a car or the trajectory of a projectile.

Horizontal and Vertical Parabolas

It's important to recognize that the axis of symmetry isn't always vertical. While most of the examples discussed revolve around parabolas opening upwards or downwards, the axis of symmetry can also be horizontal. In this case, the parabola opens to the left or right, and the equation is typically in terms of y rather than x.

The symmetry remains, but the roles of x and y are often interchanged. These horizontal parabolas appear in various applications, from architectural designs to the study of optics.

Why Does the Axis of Symmetry Matter?

The axis of symmetry is more than just a mathematical curiosity; it provides a wealth of information about the parabola. It corresponds to the symmetric line for the graph of quadratic function, which is a parabola. Knowing the axis of symmetry allows us to quickly identify the vertex, the maximum or minimum point of the parabola. The roots of the equation are disposed symmetrically with respect to this axis, which can facilitate finding the solutions.

Knowing the axis of symmetry, one can easily determine the direction of the parabola's opening. Furthermore, it simplifies graphing, as the shape of the parabola is mirrored across the axis. Thus, having a reference for the symmetry gives a lot of information about the parabola.

The Equation and Its Power

The equation of the axis of symmetry is not an abstract concept; it is a practical tool that provides direct access to the symmetrical structure of the parabola. Whether we are using the standard form, vertex form, or the x-intercepts, the underlying principles are consistent. The correct use of the formula will help you to find the axis of symmetry for any parabola, regardless of its orientation or position.

Practical Applications and Real-World Examples

The axis of symmetry is not just a mathematical concept; it is a design tool. Bridges, arches, and the shape of a car's headlights are just a few examples of where the concept is applied. In engineering and architecture, understanding the axis of symmetry is essential for achieving both structural stability and aesthetic appeal. The axis of symmetry is a fundamental concept.

The Vertex and its Relationship

The vertex of a parabola holds a special relationship to the axis of symmetry. Because the axis of symmetry passes through the vertex, finding the vertex is essential for understanding the symmetry. This reinforces the importance of the axis of symmetry.

Mastering the Concept: Practice and Problem Solving

The best way to solidify your understanding is through practice. Solving problems and working through examples will deepen your understanding. Use online calculators and interactive applets to verify your answers and visualize the concepts.

The Beauty of Symmetry

In summary, the axis of symmetry is a crucial characteristic of the parabola. It divides the curve into two symmetrical halves and intersects the parabola at its vertex. The methods to find the axis of symmetry will help you to understand and analyze a wide range of real-world scenarios and mathematical problems.

How to Find an Axis of Symmetry 11 Steps (with Pictures)

Details

Details

Detail Author:

Name : Yessenia Kirlin
Username : knikolaus
Email : fletcher.nicolas@yahoo.com
Birthdate : 1973-08-28
Address : 1258 Schowalter Crest Suite 378 Lake Stanton, KS 34508
Phone : +17694846339
Company : Littel PLC
Job : Fabric Mender
Bio : Non rerum distinctio amet libero est quia. Dicta vero perspiciatis eveniet eum asperiores. Adipisci eos id corporis excepturi consequatur odit. Et adipisci quia minus ipsam.

Socials

facebook:

url : https://facebook.com/ckub
username : ckub
bio : Nemo corrupti ut fuga commodi.
followers : 1125
following : 947

instagram:

url : https://instagram.com/chet_kub
username : chet_kub
bio : Ex quasi eum qui libero similique iste. Cumque distinctio delectus nulla voluptas non.
followers : 2593
following : 2738

tiktok:

url : https://tiktok.com/@kubc
username : kubc
bio : Facilis eligendi et quod odio. Quisquam dolorum atque dolor nihil.
followers : 6498
following : 2079

twitter:

url : https://twitter.com/chet.kub
username : chet.kub
bio : Tempora soluta est delectus facere nam. Et ut blanditiis eum nesciunt corrupti qui deserunt. Sed id qui enim cupiditate pariatur.
followers : 5908
following : 889