Learn Graphs: Types & How To Use Them | Math Guide

25 May, 2025

Ever found yourself staring at a chart and wondering what it's actually telling you? Understanding different types of graphs is like unlocking a secret language, transforming complex data into easily digestible stories.

Graphs are more than just pretty pictures; they're essential tools for making sense of the world around us. From tracking the stock market to understanding scientific data, graphs provide a visual representation that allows us to spot patterns, trends, and relationships that might be hidden in raw numbers. Whether you're a student, a professional, or simply someone curious about the world, mastering the art of interpreting graphs is a valuable skill.

Before diving into the specifics, let's quickly acknowledge the fundamental role graphs play in our understanding. In mathematics, a graph, denoted as \(g=(v,e)\), is a fundamental structure used to represent relationships between objects. Here, \(v\) represents the vertices (or nodes) and \(e\) represents the edges that connect these vertices. But the utility extends far beyond the classroom. Different types of graphs serve different purposes, each offering a unique perspective on the data they represent. The choice of graph type significantly influences how data is perceived and understood.

Let's start with some of the most common graphs you'll encounter:

Graph Type	Description	Best Use Case	Advantages	Disadvantages
Bar Graph	Uses rectangular bars to represent and compare data categories.	Comparing discrete categories, comparing groups, or tracking changes over time (with multiple bars per category).	Simple to create and understand, effective for comparing distinct categories.	Not ideal for continuous data; can become cluttered with many categories.
Line Graph	Uses points connected by lines to show trends over time or continuous data.	Tracking changes over time, illustrating trends, showing relationships between two variables.	Clearly shows trends and changes over time; can display multiple datasets on the same graph.	Can be difficult to read with many lines; less effective for comparing individual values.
Pie Chart	Represents data as slices of a circle, showing proportions of a whole.	Showing the proportions of categories that make up a whole (e.g., market share).	Visually appealing for showing proportions; easy to understand at a glance.	Difficult to compare exact values; not ideal for showing trends or changes over time; can be confusing with many small slices.
Area Graph	Similar to line graphs but with the area below the line filled in, showing cumulative values.	Illustrating the composition of multiple variables and their changes over time, showcasing cumulative totals.	Effective for emphasizing cumulative values; good for illustrating the contribution of each component to the total.	Can be difficult to interpret if too many variables are included; may obscure the data.

For more information, please check the following site:

Wikipedia: Graph (Mathematics)

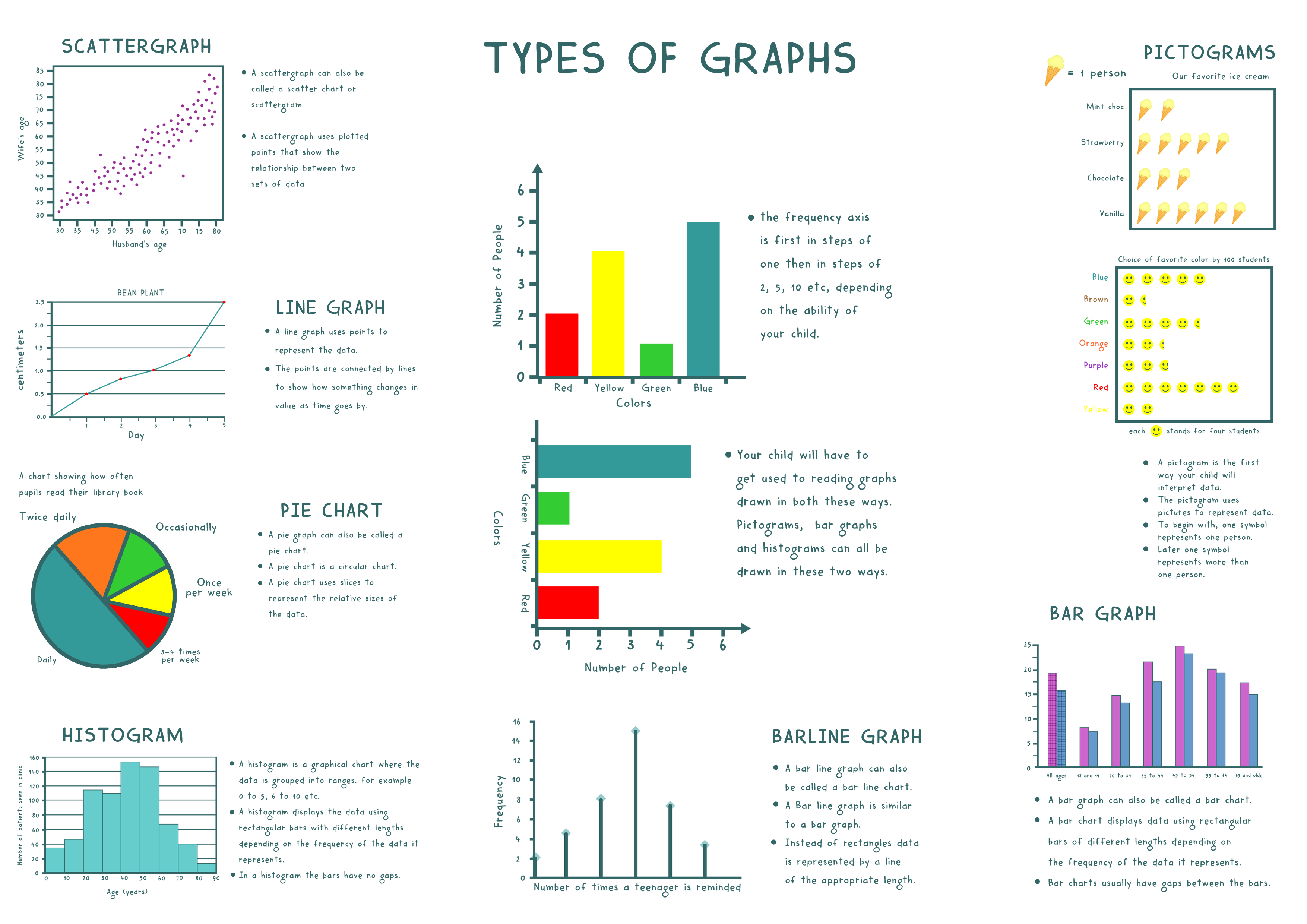
A bar graph (or bar chart) is a visual tool used to compare data across different categories. These categories are typically represented on the horizontal axis, while the vertical axis displays the values or amounts associated with each category. The length of each bar corresponds to the magnitude of the value it represents. Bar graphs are exceptionally useful for comparing discrete categories or tracking changes over a period of time. They're particularly helpful when you need to compare information collected by counting. Furthermore, the stacked bar chart, a variation, presents a detailed view by stacking bars to show 100 percent of the discrete value of each data set.

In contrast to the bar graph, a line graph is designed to illustrate trends over time or the relationship between two continuous variables. The data points are plotted and then connected by lines, allowing for easy identification of increases, decreases, and patterns in the data. The timeframe can span minutes, hours, days, months, years, decades, or even centuries. These are well suited for depicting data which changes continuously.

Pie charts, also known as circle graphs, are another visual tool, especially useful for showing proportions or percentages of a whole. Each slice of the pie represents a category, and the size of the slice corresponds to the proportion of the whole that category represents. While they are great for a quick overview of relative sizes, they are not ideal for showing changes over time or comparing precise values.

The area graph builds upon the line graph by filling in the space beneath the lines, often with colors or patterns. This visual emphasis on the area helps to represent the cumulative values of different variables over time. They are effective in illustrating the composition of multiple variables and their changes over time. This type of graph can visually demonstrate how different variables contribute to an overall total and how those contributions evolve over time. It is effective in showing both the overall trend and the individual contribution of each component.

Beyond these foundational types, there are other specialized graphs designed for specific applications:

The segmented bar chart is a type of bar chart in which each bar is divided into segments representing the components of a whole. The total length of each bar represents the total amount, and the segments show the proportions of different categories within that whole.

The Network graph is designed to illustrate relationships between different entities. These are used to visualize connections and interactions, making them especially valuable in areas like social network analysis and computer networking. They highlight connections and how different parts of a system are interconnected.

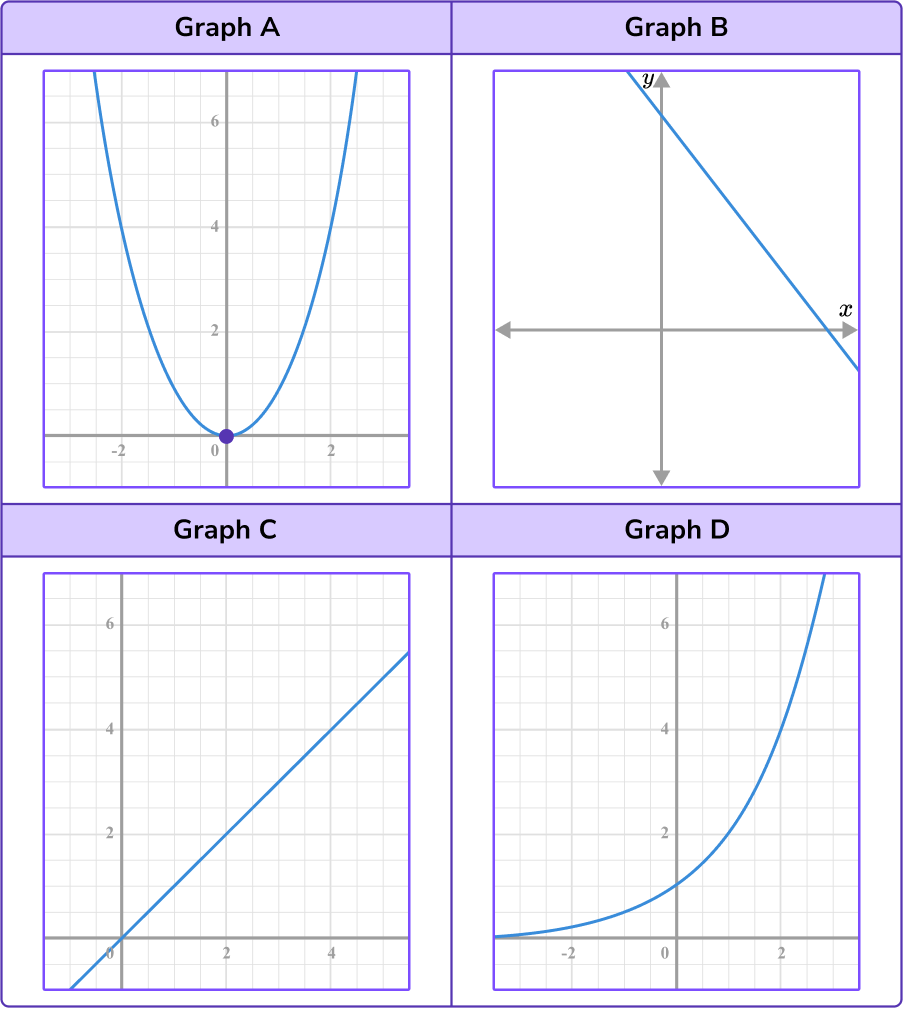
The equation of a function, \(f(x)\), dictates the shape of its graph. Different types of functions yield different graph shapes. Consider the function \(f(x) = x^2\), which produces a parabola. The shape of a graph is determined entirely by its underlying equation; the characteristics such as symmetry, asymptotes, or curvature are all derived from the function's mathematical definition.

Graphs may also contain asymptotes, which are lines that the graph approaches but never touches. Asymptotes and curves are both determined by the function's equation.

The sine wave or sinusoid, is a mathematical curve describing a smooth repetitive oscillation, named after the function sine, of which it is the graph. Trigonometric graphs, such as those of sine and cosine functions, are examples of sinusoids with varying phases, which are fundamental concepts in understanding wave phenomena and cyclical patterns.

Understanding the fundamentals of graph interpretation allows us to use these tools to draw meaningful conclusions from the data. It is possible to see trends, compare data sets, or see the distribution of a set of data by the use of the right graph.

When working with data, the choice of graph type depends on the nature of the data and the message you want to convey. Here are some general guidelines:

Use bar graphs to compare categorical or ordinal data across groups or categories. They are excellent for comparing different groups or tracking changes over a period of time.

Line graphs excel at displaying trends over time. If you need to see how something changes over a period, a line graph is a great choice.

Pie charts are perfect for displaying proportions, for example, the distribution of a budget.

Area graphs are useful for displaying the cumulative values of variables over time.

Each graph has advantages and disadvantages depending on the type of data and the purpose of the graph.

Choosing the right graph type can dramatically impact how effectively you communicate your insights. For instance, if you have data that do not continuously change over time, a bar graph is helpful to use when you have categories, and they are helpful when you need to compare information collected by counting.

The following are some key advantages and disadvantages of different graph types:

Graph Type	Advantages	Disadvantages
Bar Graph	Easy to understand, excellent for comparing discrete categories.	Not ideal for continuous data; may be cluttered with many categories.
Line Graph	Clearly shows trends over time, can display multiple datasets on the same graph.	Can be difficult to read with many lines; less effective for comparing individual values.
Pie Chart	Visually appealing for showing proportions; easy to understand at a glance.	Difficult to compare exact values; not ideal for showing trends or changes over time; can be confusing with many small slices.

The relationships between different entities can be signified by network graphs. After collecting data many times it is helpful if create a graph of this data, but what type graph should you create? There are many types of graph we can use to represent data.

In mathematics, particularly within graph theory, the term "graph" is also used in a more formal sense. A graph \(g\) is often defined as a set of vertices \(v\) and edges \(e\), written as \(g=(v,e)\). This structural definition forms the foundation for analyzing complex relationships and networks. Because graphs are so pervasive, it is useful to define different types of graphs.

The undirected graph is defined as a graph where the set of nodes are connected together, in which all the edges are bidirectional. Sometimes, this type of graph is known as the undirected network. An undirected graph is one in which its edges have no orientations, i.e., no direction is associated with any edge.

Graphs are generally used to illustrate data and different types may show the same data but the representation may be more suited to one type over another.

For a review and as a mathematical exercise, here is a quick look at how to match equations with graphs:

A cubic equation with a negative coefficient matches a specific type of curve (e.g., graph e).
A reciprocal equation with a positive coefficient matches a distinct graph (e.g., graph b).
A quadratic equation with a negative coefficient corresponds to another graph (e.g., graph c).

The use of graph analysis goes beyond basic visualization. From geometry and statistics to applied mathematics and physics, graphs are used extensively.

Types of Graphs Math Steps, Examples & Questions

Details

Types of Graphs Posters and Folder Inserts by Teach Simple

Details

Different Types Of Graphs For Statistics at Jose Cheung blog

Details

Detail Author:

Name : Amari Langosh
Username : littel.kane
Email : lawrence74@dickens.com
Birthdate : 1984-03-24
Address : 7014 Jody Points New Colemanstad, AL 33149
Phone : 1-629-483-8945
Company : Kuphal-Stehr
Job : Civil Engineer
Bio : Earum et vel et et eum laboriosam nihil qui. Et quam voluptatem nostrum reprehenderit ipsa porro. Cupiditate cumque in labore et quos.

Socials

twitter:

url : https://twitter.com/ebertd
username : ebertd
bio : Est laudantium ad dolor et aut occaecati. Voluptates voluptatem beatae est quam consequatur itaque aut. Amet inventore consequatur odio aut quo.
followers : 3545
following : 573

facebook:

url : https://facebook.com/ebert1985
username : ebert1985
bio : Rem et ex et commodi error nesciunt. Earum sed cumque nesciunt eaque et.
followers : 5784
following : 2895