Master Systems Of Equations: Methods & Solutions

22 May, 2025

Can seemingly disparate pieces of information coalesce into a cohesive whole? The answer lies within the fascinating realm of solving systems of equations, where seemingly unrelated mathematical expressions find their common ground.

When we are presented with multiple equations, each offering a unique perspective on a set of variables, we often find ourselves grappling with a complex puzzle. These equations, intertwined yet distinct, represent a system. The ultimate goal? To discover the solution(s) that satisfy every single equation within that system simultaneously.

In the world of mathematics, a solution to a system of equations isn't merely a collection of numbers; it's a specific set of values, often represented by \\(x\\) and \\(y\\), that, when substituted into each and every equation, miraculously holds true. These values provide a unique key to unlock the secrets embedded within the equations.

Various methods exist for tackling these mathematical enigmas, each offering its own strategic approach. Three primary techniques stand out: graphing, substitution, and elimination. Graphing involves visualizing each equation, looking for the points where they intersect, thus revealing potential solutions. Substitution streamlines the process by expressing one variable in terms of another, effectively simplifying the equations. Elimination, on the other hand, strategically manipulates the equations to cancel out variables, leading to a more straightforward solution.

For those venturing into the realm of linear simultaneous equations with two variables, the graphing method comes into play. The core concept is simple: plot both equations on the same set of axes. The point(s) where these lines cross is/are the solution(s) to the system. This visual approach provides a clear understanding of the interplay between equations, although it's important to remember that its precision diminishes when dealing with solutions involving decimals or fractions.

Alternatively, we can turn to the elimination method. The first step is to strategically manipulate the equations to create "opposite" coefficients for a chosen variable. Once this is achieved, adding the equations together has the effect of eliminating that variable, simplifying the equation. We then solve for the remaining variable before substituting this value back into one of the original equations to find the eliminated variable. The answer is then expressed as an ordered pair, providing a clear and concise solution.

The substitution method is yet another powerful tool in our arsenal. It simplifies a system of equations by expressing one variable in terms of another. This transforms one equation, allowing us to effectively eliminate a variable and solve the simplified equation. Once the solution is found, we can substitute the values back into one of the initial equations to obtain the value of the second variable. This streamlined approach highlights how equations work together to produce a solution.

The principles of matrices and row operations offer another perspective on solving systems of equations. To start, you write the system of equations as an augmented matrix. The matrix then undergoes a series of row operations that transform it to either row echelon form or reduced row echelon form. These row operations, such as swapping rows, multiplying rows by a constant, and adding multiples of one row to another, are designed to simplify the matrix, and ultimately, solve the system.

A crucial element in understanding any system of equations is the concept of its solution(s). A "solution" is the set of values of the unknown variables (often denoted as x and y) that simultaneously satisfy every equation within the system. These are the key numbers which, when plugged in, make all equations true, creating a harmonious balance within the mathematical context.

In practice, we often encounter systems where the equations are linear; this often means these can be represented by straight lines when graphed. These systems may have one unique solution, no solution, or infinitely many solutions. The number of solutions gives insight into the geometry of the system.

For systems of three or more variables, the approach can be extended. By using the elimination or substitution methods, we can reduce the system step by step. We start by choosing a pair of equations and solving one variable, then repeating this process with another pair. After which, we have created a smaller system, which is easier to solve.

But what if the equations don't behave linearly? What if they represent curves, not straight lines? Here, the realm of nonlinear systems comes into play. These systems, with equations that include terms like x or sin(x), introduce complexities, often with multiple solutions or more intricate interactions. These problems require careful thought as they can have several solutions and may call for advanced solving techniques.

In certain scenarios, the solutions aren't straightforward numbers but can be in the form of the point or equation. In these instances, tools such as substitution calculators are used. They help find the solution to a system of two or three equations in both point and equation forms. These tools provide a structured approach, stepping through the methods to arrive at the final answer.

When solving equations using techniques such as elimination, it is important to make the coefficients of the variables opposites. This means we can strategically add the equations to eliminate one variable. Once this happens, we can easily solve for the remaining variable. After solving for one variable, it is time to substitute the solved variable into the original equation to find the eliminated variable.

When solving any system of equations, it's important to remember that we are ultimately searching for a set of values that simultaneously make all equations within the system true. These values may or may not be whole numbers, but they provide the key to understanding the relationship between each equation.

Finally, in the application of these techniques, there are various software tools available. Some of these tools offer guidance, steps, and feedback. These can be helpful for understanding the principles and practicing systems of equations. Ultimately, the key to mastering the system is the ability to combine techniques with an analytical, systematic approach.

Consider the scenario where someone, for example, Sondra, is mixing drinks. She needs to determine the right proportions of ingredients to create a specific cocktail. The situation may transform into a system of equations. Let's assume she needs a specific volume of a beverage and that it is made of club soda (represented as s) and another ingredient (represented by f). The solution, the precise measurement of each ingredient, will need to satisfy the set volume. For example, the equation may look like this: -2f - s = -16. In this context, the solution isn't just abstract numbers; it represents the real-world quantities of each ingredient Sondra needs to use. The point of intersection (2, 8) is the solution, so sondra needs 2 quarts of club soda and 8 quarts of other ingredient.

Method	Description
Graphing	Plot each equation on a graph; the intersection point(s) represent the solution(s).
Substitution	Solve one equation for a variable, then substitute that expression into the other equation.
Elimination	Manipulate the equations to eliminate one variable by adding or subtracting the equations.
Matrices	Represent the system as an augmented matrix, use row operations to simplify.

In summary, solving systems of equations is much more than a mathematical exercise; it is a versatile skill used to analyze information, make informed decisions, and model various real-world scenarios.

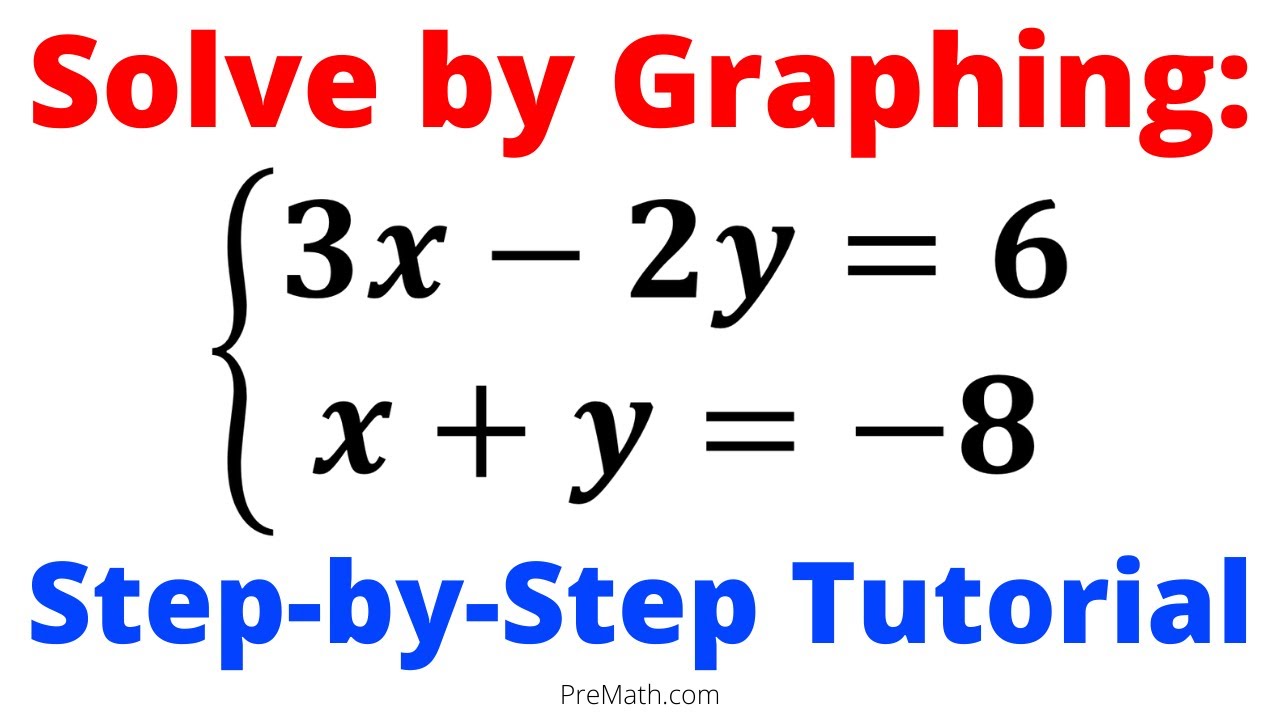
How to Solve a System of Equations using the Graphing Method Fast

Details

Use this QUICK TRICK to Solve a System of Equations Fast & Easy

Details

QUICK TRICK for Solving Systems of Equations Save Time & Energy

Details

Detail Author:

Name : Milton O'Hara V
Username : erin46
Email : enos05@hotmail.com
Birthdate : 1987-08-06
Address : 25913 Prosacco Land Apt. 969 Willieland, TX 85609
Phone : +1-631-413-5484
Company : Moen-Padberg
Job : Legislator
Bio : Consequatur vero consequatur quia praesentium in. Voluptates neque quas nemo quia vel libero. Praesentium iure distinctio voluptas asperiores ipsum dolorem. Eius aliquam voluptatum id sapiente.

Socials

tiktok:

url : https://tiktok.com/@jarret_von
username : jarret_von
bio : Nihil aut tenetur veniam amet incidunt occaecati dolorem.
followers : 885
following : 596

twitter:

url : https://twitter.com/jarret_id
username : jarret_id
bio : Ea dignissimos eum dolorem sequi inventore. Fugiat et minus necessitatibus quis quia consequuntur. Corporis officia dolorem ipsam eos occaecati dolor.
followers : 2645
following : 2751