Math Help: Solving Equations & Simplifying Expressions With ["\\times..."]

20 May, 2025

Can the complexities of mathematics be tamed and made accessible to everyone? The answer, surprisingly, is a resounding yes, thanks to a convergence of innovative tools and a renewed focus on clear, concise explanations. This journey into the world of numbers, equations, and calculations reveals a landscape where understanding is not just possible but easily attainable, transforming the way we approach and appreciate mathematics.

The core of this transformation lies in understanding the fundamental building blocks of mathematical thought. These building blocks are not just the formulas and theorems; they are the concepts that underpin them. For instance, consider the cartesian product, denoted by the symbol "\\times." This seemingly abstract concept is not as daunting as it initially appears. When we encounter "\\times is the cartesian product and [0,m] is the interval \\{x:0 \\le x \\le m\\}," we're introduced to a framework. The cartesian product combines elements from two sets, creating ordered pairs. Specifically, x \\times [0,m] = \\{(x,r):x \\in x \\land 0 \\le r \\le m\\} for y. This statement can be thought of in terms of combining each value of x with all the values in an interval from 0 to m. This is a cornerstone for many advanced mathematical concepts.

In the realm of practical application, consider the power of a "solve for x calculator." This tool demystifies equations. Whether the equation involves one variable or many, the calculator provides immediate solutions. Expressions like "7x and 3x are like terms because they both contain x" are easily manageable. The key is to identify like terms in an expression, add or subtract their coefficients, and then rewrite the expression with combined terms. For instance, "Combine the like terms (4x and \u22122x):" and "Combine constants (5 and 3;" lead to a simplified solution. The process emphasizes the core logic of solving equations, breaking it down into manageable steps.

The "equations section" offers the ability to solve an equation or system of equations. This tool can yield the exact answer, or, if needed, a numerical answer to the required degree of accuracy. A user simply enters their expression to be evaluated, and the math calculator produces the final solution. Further, calculations are not limited to solving equations. You can also use the calculator for arithmetic, subtraction, multiplication, and division. For example, given an expression with three indeterminates such as "x + 2xyz \u2212 yz + 1," the calculator can simplify it to reveal the underlying structure.

A "quadratic equation in mathematics" is a concept central to many fields. Defined as an equation of the form "displaystyleax\u00b2+bx+c=0," it introduces concepts of variables and constants. Where the variable x represents an unknown number and a, b, and c represent known numbers, with a \u2260 0. Understanding this structure allows for tackling complex problems.

Beyond the immediate solutions, the ability to combine terms that aren\u2019t like terms is vital. For example, "When solving for x, only terms with x can be combined with each other." Combining like terms, like "4x and 7x make 11x" streamlines the process. Then we can use a simplification calculator, taking complex expressions and reducing them to their simplest form.

Moreover, math notebooks have existed for centuries. This approach is a nod to the power of documenting the problem-solving process step-by-step. The process includes identifying relevant information, defining variables, and planning a strategy. By breaking down the complexity, each step becomes easier to understand. The process may include clicking "go" after entering an expression and obtaining an immediate simplified version of that expression. The focus is on the learning process. The goal isn't just the final result; rather, it's the process that happens just below the surface.

Now, let's delve into specific numerical problems. The seemingly simple question, "What is 5 times 64?" highlights the importance of mastering basic arithmetic. Likewise, "What is (x + 5) times (x + 5)?" introduces algebraic expressions. Exploring more complex examples, such as "What is 2x times x?" or "What is 2 times 3?" establishes the importance of both arithmetic and algebraic principles. Evaluating "What is 4.14 times 10^2?" showcases the need for working with exponents. Tackling larger sums, such as "What is 50 times 15?" or "What is 38 times 2?" strengthens our mastery of these skills. Finally, the question "What is 6 times 6 times 6?" provides a chance to build on these fundamental skills. Further, the exploration of "7.08 times 10^15 or 7.65 times 10^14 or 7.65 times 10^4;" introduces the process of scientific notation.

Understanding integrals requires a certain amount of training. "\\int f(x)dx" represents the complete class of integral. Also, the constant "C is an arbitrary constant." Additionally, "X is the variable of equation" and the symbol "$\\int$ denotes the integral." The concept of exponents, where "Exponents are numbers representing the power to which a number or variable is raised," expands the range of mathematical tools at our disposal. By knowing exponents and learning about the specific rules, we are able to address more difficult problems. Also, using online graphing calculators to visualize equations and plot points promotes greater understanding.

In summary, the journey of learning mathematics is far from a daunting path. By exploring fundamental concepts, utilizing tools and techniques, and by appreciating the beauty of the process, everyone can achieve mathematical mastery.

Let's explore a simple example: When you multiply 4x by x, you are essentially multiplying 4 by x and then multiplying the result by x again. This can be written as: To simplify this, you multiply the coefficients (the numbers) and then multiply the variables (the x\u2019s). 4 \u00d7 1 = 4. X \u00d7 x = x\u00b2

By utilizing an "online math solver with free step by step solutions to algebra, calculus, and other math problems" we can seek help. We can also seek assistance on the web or with our math app. "Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more." Moreover, a "root is a value for which the function equals zero."

Consider the equation "Write an equation for three times a number increased by 32 is the same as four times the number decreased by 15 find the nu?". With our combined knowledge, we can solve this problem, transforming mathematical anxiety into empowerment.

Multiplication Table Chart Mathematics, PNG, 2481x3508px

Details

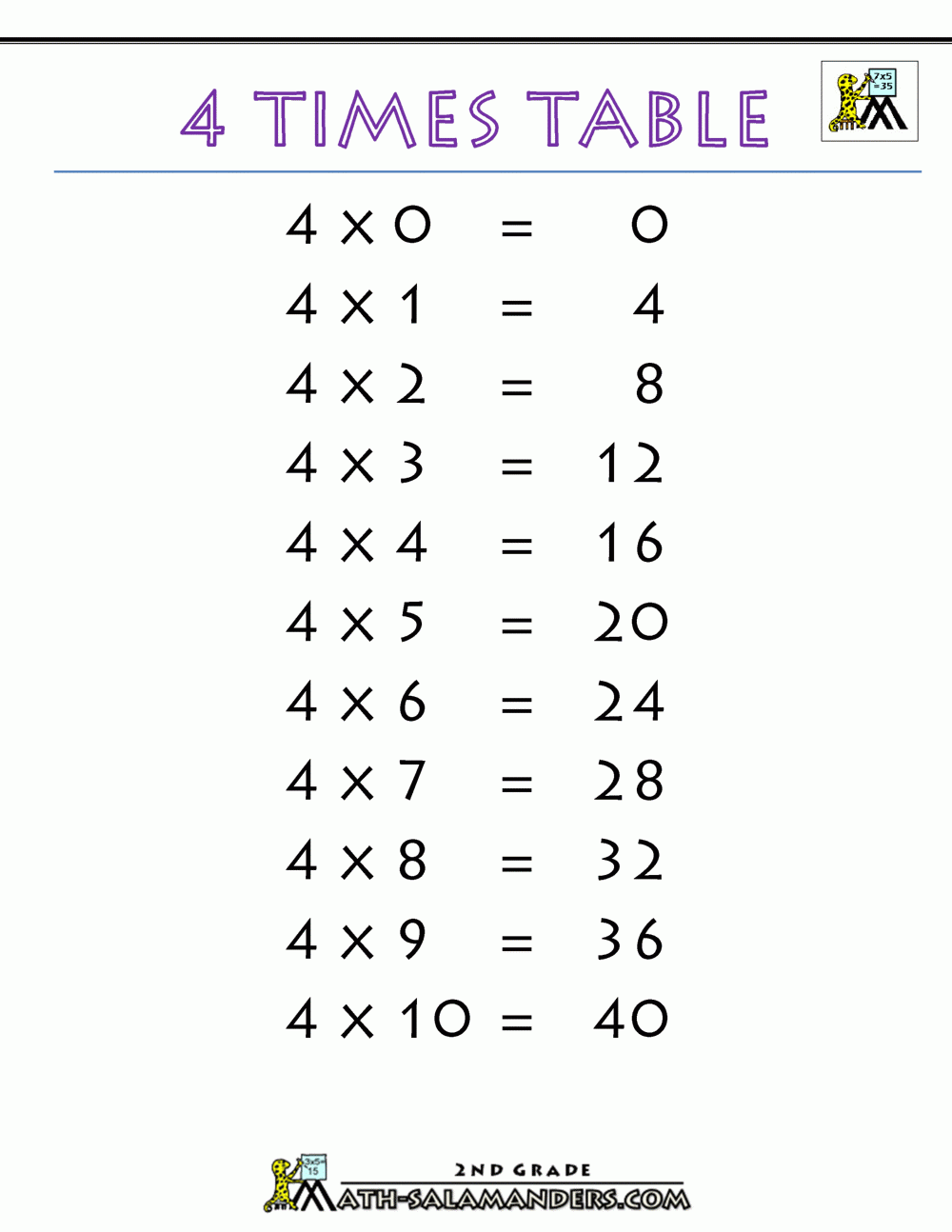
4X Times Tables Worksheets Free Printable

Details

Details

Detail Author:

Name : Milton O'Hara V
Username : erin46
Email : enos05@hotmail.com
Birthdate : 1987-08-06
Address : 25913 Prosacco Land Apt. 969 Willieland, TX 85609
Phone : +1-631-413-5484
Company : Moen-Padberg
Job : Legislator
Bio : Consequatur vero consequatur quia praesentium in. Voluptates neque quas nemo quia vel libero. Praesentium iure distinctio voluptas asperiores ipsum dolorem. Eius aliquam voluptatum id sapiente.

Socials

tiktok:

url : https://tiktok.com/@jarret_von
username : jarret_von
bio : Nihil aut tenetur veniam amet incidunt occaecati dolorem.
followers : 885
following : 596

twitter:

url : https://twitter.com/jarret_id
username : jarret_id
bio : Ea dignissimos eum dolorem sequi inventore. Fugiat et minus necessitatibus quis quia consequuntur. Corporis officia dolorem ipsam eos occaecati dolor.
followers : 2645
following : 2751