Solving Linear Equations: The Power Of Graphing Learn Now!

25 May, 2025

Can solving equations be as simple as drawing lines? Graphing offers a remarkably intuitive and visual approach to unraveling the complexities of systems of linear equations, providing unparalleled insights into the interconnectedness of these mathematical relationships.

The world of mathematics is often perceived as an abstract realm of symbols and equations. However, beneath the surface lies a world of visual representation and intuitive understanding. Graphing, as a method for solving systems of linear equations, exemplifies this beautifully. It transforms abstract algebraic concepts into tangible visual forms, enabling a deeper comprehension of the relationships between equations. While other methods, such as substitution or elimination, may offer greater precision in certain scenarios, graphing stands out as a powerful tool for beginners and seasoned mathematicians alike. It offers a straightforward pathway to understanding the fundamental principles that govern these systems.

The essence of solving systems of equations graphically lies in recognizing that a system of equations is essentially a collection of two or more equations, all sharing the same set of unknown variables. The core objective is to pinpoint the values for these unknowns that satisfy every equation within the system. Each equation, in the realm of linear equations, is intrinsically linked to a line. This implies that when you solve a system containing two linear equations, you are essentially dealing with two lines, and the solution, if it exists, manifests as a single ordered pairthe point where these lines intersect.

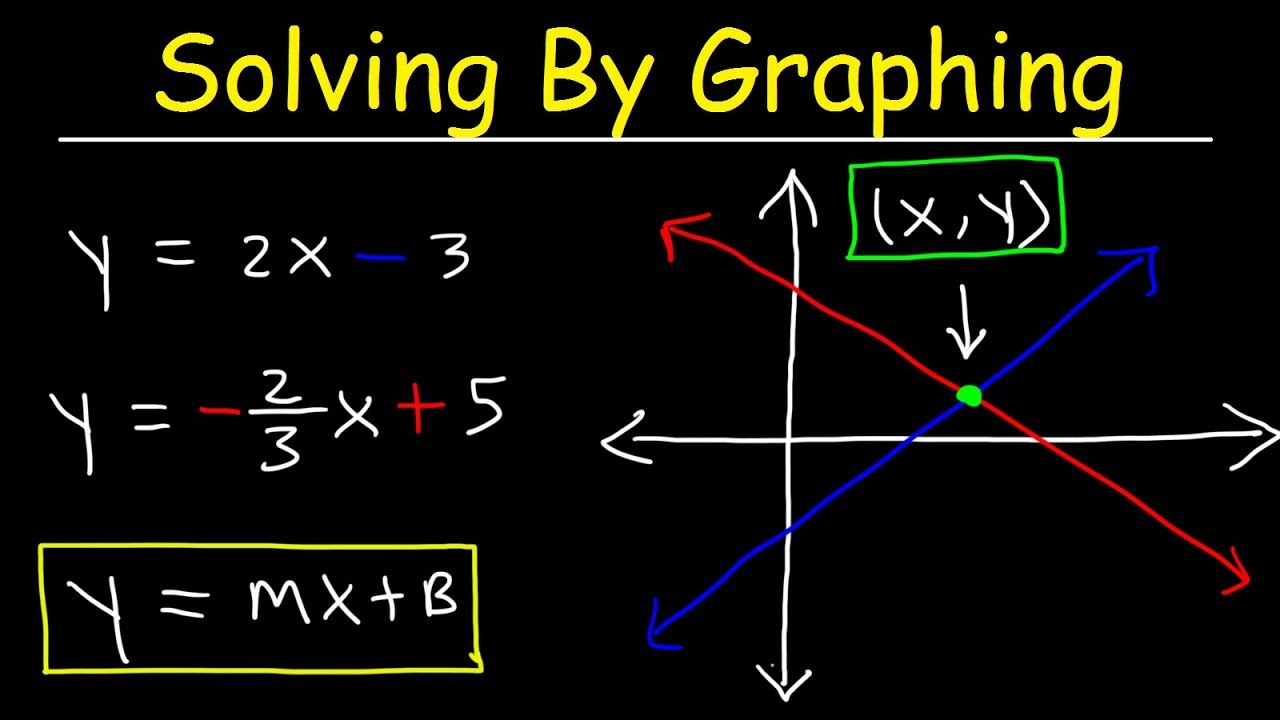
To tackle systems of equations through graphical means, it's crucial to address each line individually. This involves analyzing the equation that defines the line, determining its slope and y-intercept, and plotting it accurately on a coordinate plane. Only then can the interplay between multiple equations be understood. Graphing simplifies the process. Graphing a system of linear equations is as simple as graphing two straight lines, the solution lies at the point of intersection.

Graphing systems of equations is a fundamental concept introduced in the 8th grade when students first encounter linear systems. At this stage, students begin to appreciate the visual aspect of mathematics and how different equations are connected. The value of graphical representations becomes evident as students move from abstract concepts to concrete visualizations.

For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes. This approach provides a clear visual representation of the relationships between the equations. You will learn how to solve a system of equations by graphing, including linear and nonlinear systems. You will also learn how to interpret graphs to identify solutions. This method is best for beginners.

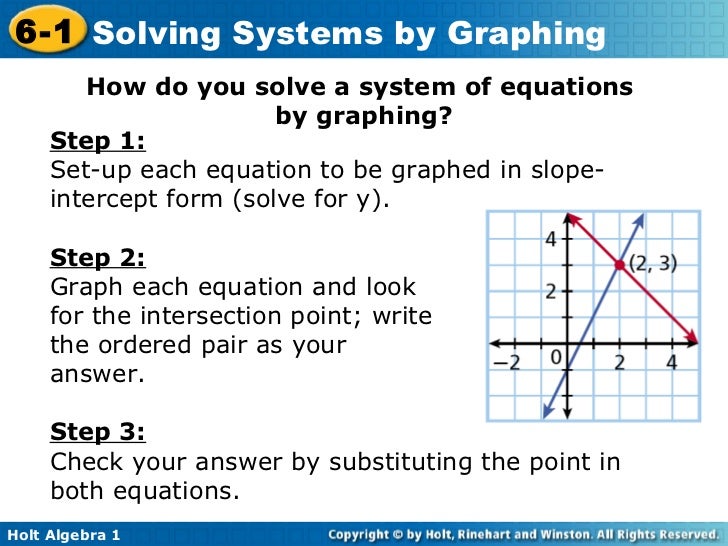
When it comes to the nitty-gritty of solving systems of equations graphically, certain steps become indispensable. The first step is to rearrange the equations so they read y = form. This format allows for direct identification of the slope and y-intercept, the two essential elements needed to draw a line on the coordinate plane. Next, the equations should be graphed on the same set of axes. The solution to the system is revealed where the lines intersect, represented as an (x, y) ordered pair.

Its crucial to understand that not all systems of equations have one unique solution. Sometimes, the lines representing the equations might be parallel, indicating no solution. Other times, the lines may coincide, meaning that there are infinitely many solutions. The graphical approach provides a clear visual representation of these scenarios, enabling students to grasp the diverse possibilities inherent in solving systems of equations.

The limitations of graphical solutions, such as precision, are also a critical part of understanding its role. While graphing offers an intuitive understanding, it might not always yield highly precise solutions, especially when dealing with complex equations or fractional solutions. In such cases, other algebraic methods might prove more efficient. Still, students learn about the limitations of graphical solutions, such as precision.

When using the graphing method to solve a system of linear equations, we can imagine each equation as a path, and the solution is where the two paths intersect. This algebra video tutorial explains how to solve systems of equations by graphing. The solution is the point of intersection of the two graphs.

In essence, graphing provides an accessible entry point into the world of systems of equations, equipping learners with a foundational understanding of the concepts and relationships involved. Graphing also offers a solid basis upon which to explore other methods, such as substitution and elimination.

Let's consider how these concepts manifest in practice. Imagine a system of two linear equations. The first step involves rearranging the equations into slope-intercept form (y = mx + b). The second step is to plot both equations on the same coordinate plane. The point where the lines intersect is the solution. The solution must satisfy every equation in the system.

This method is excellent because it provides an intuitive understanding. It offers a visual representation of algebraic concepts. It also helps students to develop problem-solving skills and a strong foundation in linear algebra. It offers a hands-on approach.

Understanding the nature of solutions single solutions, no solutions, or infinite solutions is a fundamental aspect of grasping systems of equations. When the lines intersect at a single point, there is precisely one solution. When the lines are parallel, there is no solution. When the lines coincide (lie on top of each other), there are infinitely many solutions.

In the wider context of mathematics, the ability to solve systems of equations is a critical skill that extends beyond simple equations. It is a skill that helps in various fields of study.

In the classroom, you would apply the following steps. The first step would be to graph each equation. The next step would be to locate the intersection point. Last step is to check your solution.

In summary, graphing is a crucial tool for solving systems of linear equations. It not only provides a visual understanding of algebraic concepts but also enhances problem-solving skills and establishes a strong foundation in mathematics. From the initial steps of graphing simple equations to analyzing complex systems, the ability to visualize and interpret graphical representations is an indispensable asset in the world of mathematics.

How To Solve Systems Of Linear Equations

Details

Details

A1, 6 1, solving systems by graphing (blog 1)

Details

Detail Author:

Name : Brennan Harvey
Username : asha81
Email : turner80@gmail.com
Birthdate : 1998-12-17
Address : 62843 Alvena Loaf South Cortezberg, SD 52392-0320
Phone : +15802009511
Company : Cartwright, Leffler and Daniel
Job : Management Analyst
Bio : Fuga ab consequatur ut doloribus labore a vel nobis. Accusamus eum vel sed. Occaecati consequuntur occaecati repellendus aliquid commodi voluptas. Numquam ut magni neque eum numquam suscipit.

Socials

instagram:

url : https://instagram.com/ltreutel
username : ltreutel
bio : Assumenda enim quia eum omnis ut. Ea culpa ullam eveniet nihil vitae.
followers : 6341
following : 1876

tiktok:

url : https://tiktok.com/@leta_id
username : leta_id
bio : Labore et nisi enim cum voluptatem. Quae voluptatum neque ullam in commodi.
followers : 724
following : 767

twitter:

url : https://twitter.com/ltreutel
username : ltreutel
bio : A aut qui et recusandae. Officiis velit amet quis velit. Harum voluptatum tenetur aut ratione ipsam ratione tenetur.
followers : 2230
following : 706