Understanding Constants In Math: Definitions, Examples & Uses

24 May, 2025

Ever wondered what underpins the seemingly chaotic world of mathematics, providing stability and predictability? The answer lies in constants the unwavering anchors in a sea of variables. These are the fundamental building blocks that give structure and meaning to equations, formulas, and the very fabric of reality as we understand it.

A constant, in its simplest definition, is a fixed value that does not change. This immutable quality is what sets it apart from variables, which are symbols representing values that can vary. Constants can be numbers, like 2, -5, or 3.14159, or they can be represented by symbols, such as (pi), which represents the ratio of a circle's circumference to its diameter, or e, the base of the natural logarithm.

Category	Detail
Name	Constant
Definition	A fixed value that does not change in a mathematical expression or equation.
Types	Mathematical, Numerical, Symbolic, Constant Terms, Constant of Proportionality, Constant Functions
Examples	0 (pi) 3.14159 e 2.71828 Speed of light (approximately 299,792,458 meters per second)
Usage	Algebra Geometry Physics Calculus Economics
Key Properties	Unchangeable, Fixed, Immutable, Essential for Defining Relationships and Solving Equations
Related Concepts	Variables Coefficients Parameters Functions Proportionality
Reference	Wikipedia - Constant (Mathematics)

The significance of constants extends far beyond the classroom. In physics, for instance, the speed of light is a fundamental constant, a cornerstone of Einstein's theory of relativity. This constant, approximately 299,792,458 meters per second, dictates the ultimate speed limit in the universe, influencing our understanding of space, time, and energy. The gravitational constant, another key figure in physics, governs the attraction between objects with mass, shaping the orbits of planets and the structure of galaxies.

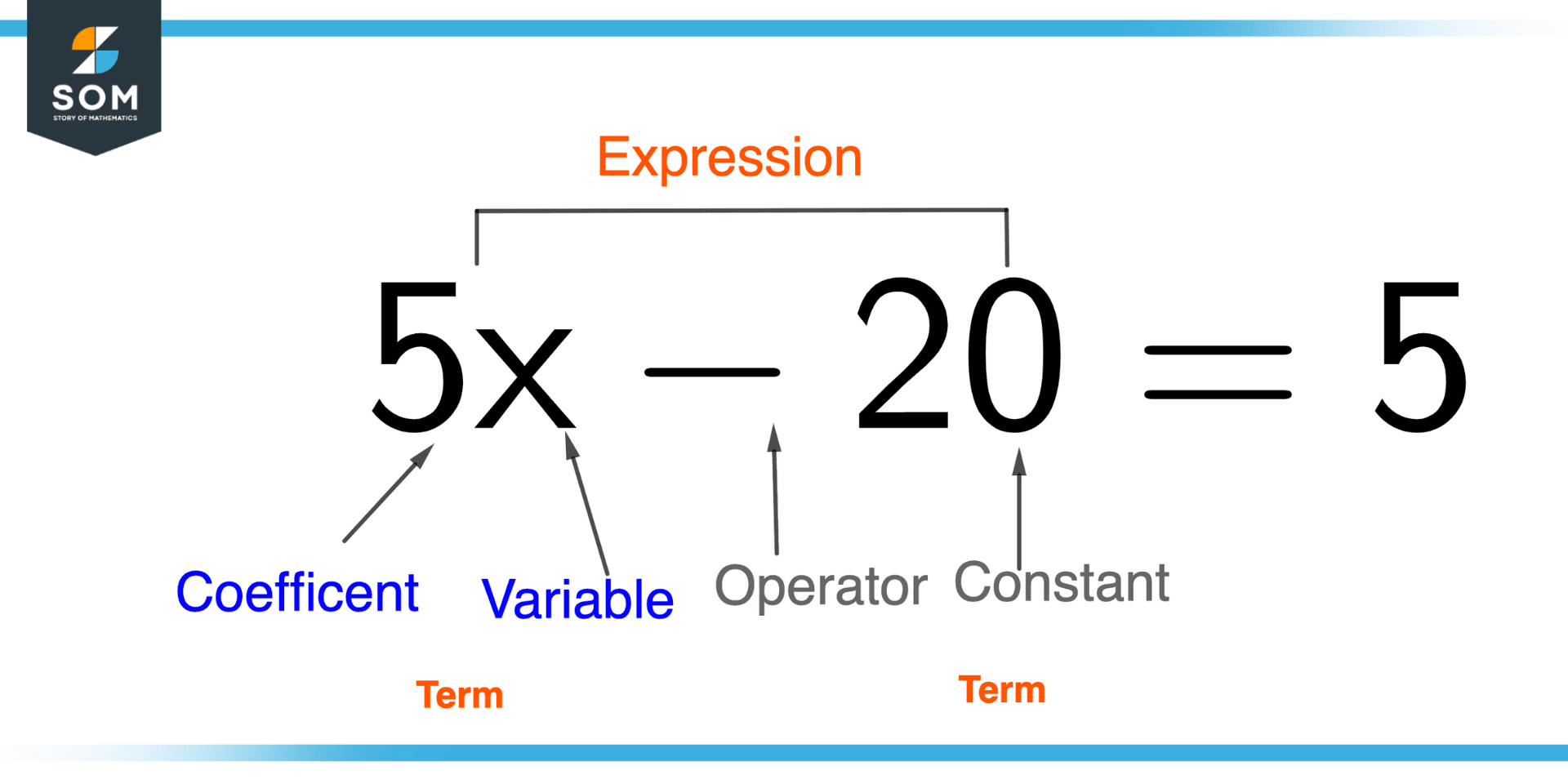
In algebraic expressions, constants play a crucial role in defining relationships and solving equations. Consider the simple equation: x + 5 = 10. In this instance, 5 and 10 are constants. While 'x' is a variable, the constant 5 acts as a fixed value, and the equation aims to determine the value of 'x' that makes the equation true given the constant values. The constant term in an algebraic expression is the term that does not contain any variables; for example, in the quadratic polynomial x + 2x + 3, the number 3 is a constant term. It is a value that remains unchanged, regardless of the values of any variables in the expression.

Mathematical constants, often represented by symbols, are key numbers whose values are defined precisely and are used repeatedly across various mathematical problems. Pi (), for example, is a mathematical constant that represents the ratio of a circle's circumference to its diameter. The circumference of a circle with a diameter of 1 is exactly . This constant is fundamental in geometry and is used extensively in calculations involving circles, spheres, and other circular shapes. Another important constant, e, approximately equal to 2.71828, is the base of the natural logarithm and is central to exponential growth and decay models, found in fields from finance to biology.

Constants are not confined to the realm of pure numbers. They can also be found in various contexts, serving different purposes. In economics, the constant rate of change is used to describe the relationship between supply and demand. The constant of proportionality is the constant generated when two variables form a direct or inverse relationship. If two quantities, x and y, are directly proportional, the relationship can be expressed as y = kx, where k is the constant of proportionality. The value of k remains constant, irrespective of the values of x and y. For example, if you are paid $20 an hour, the constant of proportionality is 20, because your pay equals 20 multiplied by the number of hours worked.

Constant functions are a specific type of function where the output is always the same, regardless of the input. These functions take the form f(x) = k, where 'k' is a constant. This means that no matter what value you plug into the function for 'x', the output will always be 'k'. For instance, if f(x) = 7, then f(1) = 7, f(10) = 7, and f(-5) = 7. The graph of a constant function is a horizontal line.

Understanding constants is essential for anyone venturing into mathematics or related fields. They provide stability, allowing us to build more complex concepts and models. Without constants, our ability to understand and predict the world around us would be severely limited. They are the unchanging foundation upon which so much knowledge is built.

In summary, a constant is an unchangeable quantity in mathematics. Its a value that does not alter over time or in response to different input values. Constants are used to represent fixed values that do not change, like the gravitational constant and the speed of light. They are the bedrock of many mathematical concepts, equations, and formulas, enabling us to build complex models and relationships. From the fundamental constants of physics, to the parameters in economic models, and the unwavering values within mathematical expressions, constants underpin the very structure of our understanding. They offer a sense of order and predictability in a world of variables, playing an indispensable role in our quest to understand the universe.

The concept of constants continues to play a vital role in modern mathematics. They are used throughout various mathematical branches like algebra, geometry, physics, and calculus. Constants will forever remain fundamental to mathematics.

What is a Constant Definition of Constant

Details

Details

Details

Detail Author:

Name : Roman Kihn
Username : erdman.luis
Email : larson.madie@gmail.com
Birthdate : 1999-07-05
Address : 778 Haley Junction East Pauline, ND 81801
Phone : +1-952-274-4742
Company : Turner-Wyman
Job : Hunter and Trapper
Bio : Totam est repudiandae molestiae soluta amet rerum. Doloribus dolor dolor minus unde voluptatum consequatur fugit. Et ut rerum voluptatem voluptatem nam.

Socials

twitter:

url : https://twitter.com/predovic2015
username : predovic2015
bio : Quas consequuntur totam pariatur rerum dolorum rerum est. Laboriosam odit culpa ea fuga et non ut. Quibusdam ipsam neque cumque tempore tempore.
followers : 4928
following : 1273

instagram:

url : https://instagram.com/al.predovic
username : al.predovic
bio : Enim occaecati nemo inventore et consequatur fuga. Et quis in cupiditate aut sint quos.
followers : 3112
following : 1931