Understanding Cube Roots: Definitions, Examples & Calculations

24 May, 2025

Ever wondered what lies at the heart of mathematical precision, the core principle that underpins complex calculations and unlocks the secrets of numbers? A root, a seemingly simple concept, is actually the cornerstone of a vast array of mathematical concepts, representing a value where a function gracefully touches zero.

In the realm of mathematics, particularly algebra, the cube root emerges as a fundamental operation. Unlike its simpler cousin, the square root, which seeks a value that, when multiplied by itself, yields the original number, the cube root delves deeper. It searches for a value that, when multiplied by itself three times, returns the original number. This is mathematically expressed as: if \( x^3 = y \), then \( x \) is the cube root of \( y \).

Simplifying expressions involving cube roots involves a delicate dance with radicals and exponents. For instance, simplifying the cube root of x to the power of 4 (\(\sqrt[3]{x^4}\)) requires factoring and extracting terms from under the radical. This might involve rewriting the expression to highlight perfect cubes, or using the property that the cube root of a product is the product of the cube roots.

Consider the following example of simplifying an expression involving cube roots: 3 \(\sqrt{x^4}\). You can pull terms out from under the radical, factor out x , or utilize the properties of exponents to arrive at a simplified form. The manipulation of these expressions hinges on a strong understanding of exponents and radicals.

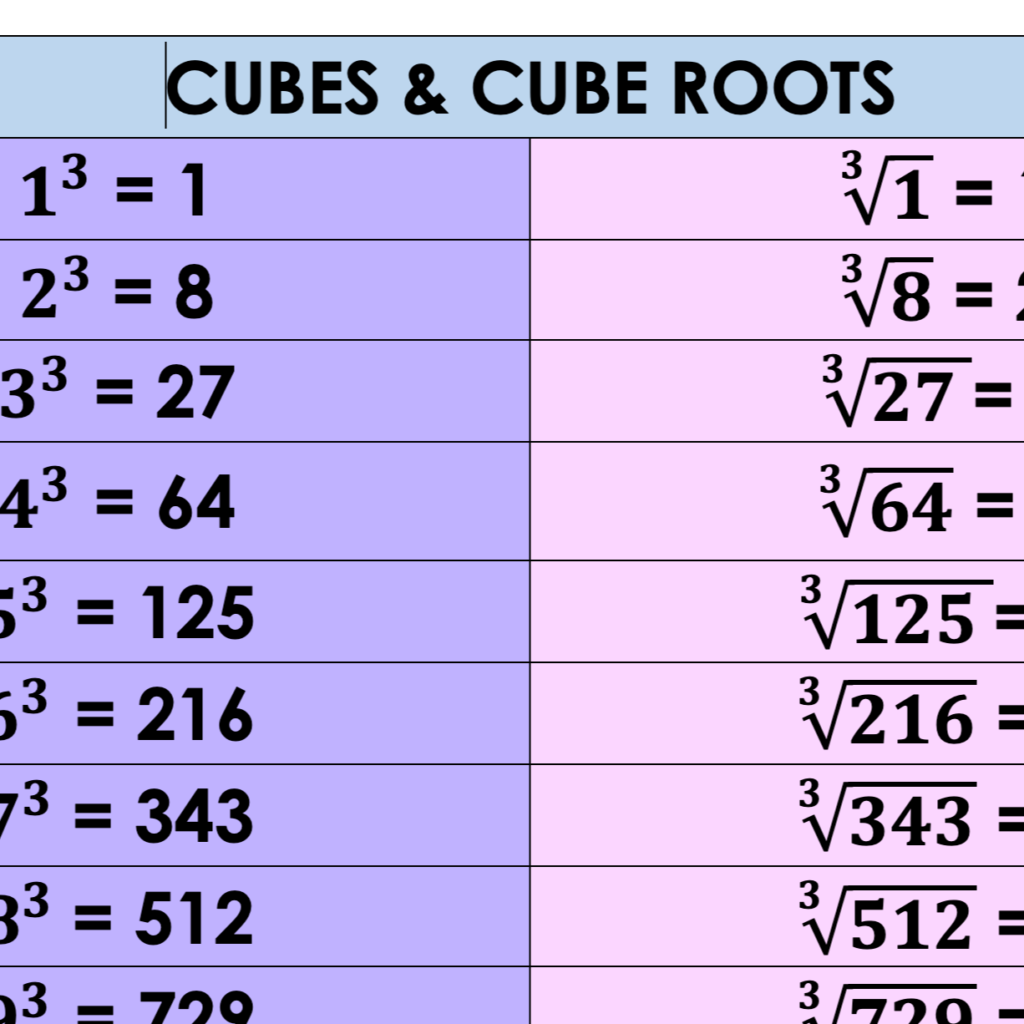
The concept of the cube root is often contrasted with the ease of working with perfect cubes. Perfect cubes are numbers that result from cubing an integer (e.g., 8 is a perfect cube because 2 = 8). Finding the cube root of a perfect cube is straightforward, yielding an integer result. However, determining the cube root of a non-perfect cube, like 30, poses a greater challenge.

Consider the question: What is the cube root of 30? While it is easy to recognize that the answer lies between 3 and 4, as 3 3 3 = 27 and 4 4 4 = 64, the exact value isn't immediately apparent. This highlights the distinction between perfect cubes and non-perfect cubes.

In contrast, finding the cube root of a number which is not a perfect cube can yield a non-integer value. Take, for example, the cube root of 4. While this can be expressed in radical form, it is not an integer, illustrating the complexities that can arise with this mathematical operation.

The cube root, in essence, is the inverse operation of the cubing process, or raising a number to the power of 3 (\(x^3\)). The inverse of the cube root of 4.5, is of course, the operation of raising a number to the power of 3, but it requires further calculation to determine the actual value of that number.

In the context of mathematics, the components of radical expressions are meticulously defined. For instance, in the expression \(\sqrt[3]{8} = 2\), the '3' is the index, the symbol \( \sqrt{} \) is the radical symbol, and '8' is the radicand. The cube root of 8 is 2, as 2 2 2 = 8.

Let's consider the concept of cube root in terms of its exponent representation. The cube root of a number 'x' is equivalent to 'x' raised to the power of 1/3. This duality allows for flexibility in mathematical manipulations, and helps one to understand it in terms of powers. In other words, the cube root of 'x' can be expressed as \( x^{\frac{1}{3}} \).

The value of the cube root of 4, when rounded to six decimal places, is approximately 1.587401. This is the real solution to the equation \(x^3 = 4\). It is an irrational number. This emphasizes the fact that these roots can often be approximations, especially when dealing with non-perfect cubes.

The cube root of 4 is expressed as \(\sqrt[3]{4}\) in radical form, and as \((4)^{\frac{1}{3}}\) or \((4)^{0.333}\) in exponent form. Each representation offers a different perspective on the same mathematical concept, allowing us to approach the problem from various angles.

Calculating the cube root of 4 can be done using various methods, including Halley's method, as well as calculators or the radical symbol. The value of the cube root of 4 is approximately 1.5874, it is an irrational number. This means it cannot be expressed as a simple fraction, and its decimal representation goes on forever without repeating. Understanding the properties of the cube root of 4 means being able to recognize it as an irrational number.

Estimating roots by hand can be done using simple methods. If 4 is not a perfect cube, it is an irrational number and cannot be represented as a simple fraction, which in turn means it's not a rational number.

When considering the cube root of 4-digit numbers, the process remains the same, but the calculations are more involved. One can use prime factorization, estimation and approximation methods to find the cube root, as the process and concept remains the same.

The concept extends beyond simple examples. For instance, when calculating the square root of a radical expression, we use a square root calculator to find the square root. The key concept is the inverse operation and the properties of roots.

It's also important to note that, the real number cube root is the principal cube root, and each real number cube root (zero excluded) also has a pair of complex conjugate roots.

To calculate any root of a number, you can use our nth root calculator. If you're dealing with complex or imaginary solutions, you may need to simplify radical expressions using a specialized calculator.

The square root of a number 'x' is a value 'y' such that \(y^2 = x\). The square root is denoted by \(\sqrt{x}\).

For example, \(\sqrt{16} = 4\) because \(4^2 = 16\).

One of the fundamental properties of square roots is that the square root of a product is equal to the product of the square roots. This can be written mathematically as: \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\)

In contrast to the cube root, notice that there is no small number (the index) in the square root symbol (often the number 2 is implied). The symbol for the square root can also be written with a 2 instead of a 3, for clarity.

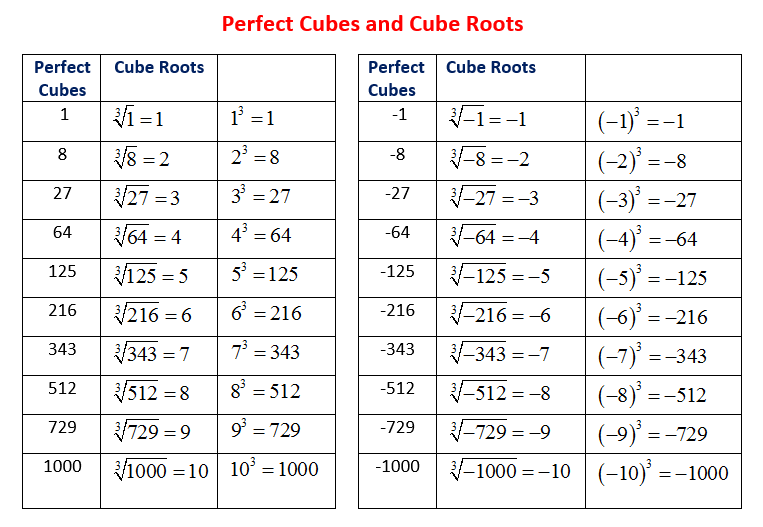
Knowing that even natural numbers' cube root is always even, and that all odd numbers' cube root is odd, can help quickly identify if your solution is in the right range. For example, the cube root of 8 is 2, the cube root of 64 is 4, etc.

All negative integer cube roots are always in negative integers. The cube root calculator reduces any cube root to its simplest radical form as well as provide a brute force rounded approximation. Understanding these patterns is key to working with cube roots.

Consider the cube root of 4 again. We know that the prime factorization of 4 is \(2 \cdot 2\). Thus, we get an irrational number that is approximately equal to 1.587401. Understanding the prime factorization of a number helps determine its cube root. The cube root of 4 is represented as \(\sqrt[3]{4} \approx 1.5874\).

Consider how to find the cube root of 64. We can use the prime factorization method. 64 = 2 2 2 2 2 2 = 4 4 4 = 4. Then, taking the cube root on both sides gives us the cube root of 64 is 4.

Square roots also share the same properties as cube roots. The symbol for the square root can also be written with a 2 instead of a 3, but it's commonly not shown as square roots are the most used. So, if there is no small number (the index) indicated, you are dealing with a square root.

Let's dive deeper into the simplification process for the cube root of 4. We know that \(4 = 2 \cdot 2\). Therefore, \(\sqrt[3]{4} = \sqrt[3]{2 \cdot 2}\) which is already in the simplest form and approximately equals 1.5874010519682 (in decimal form).

The 4th root of 81 can be written as \(\sqrt[4]{81} = \pm 3\), and the 5th root of 1024 is written as \(\sqrt[5]{1024} = 4\).

Understanding the concept of roots and their applications unlocks a new level of understanding of many aspects of math.

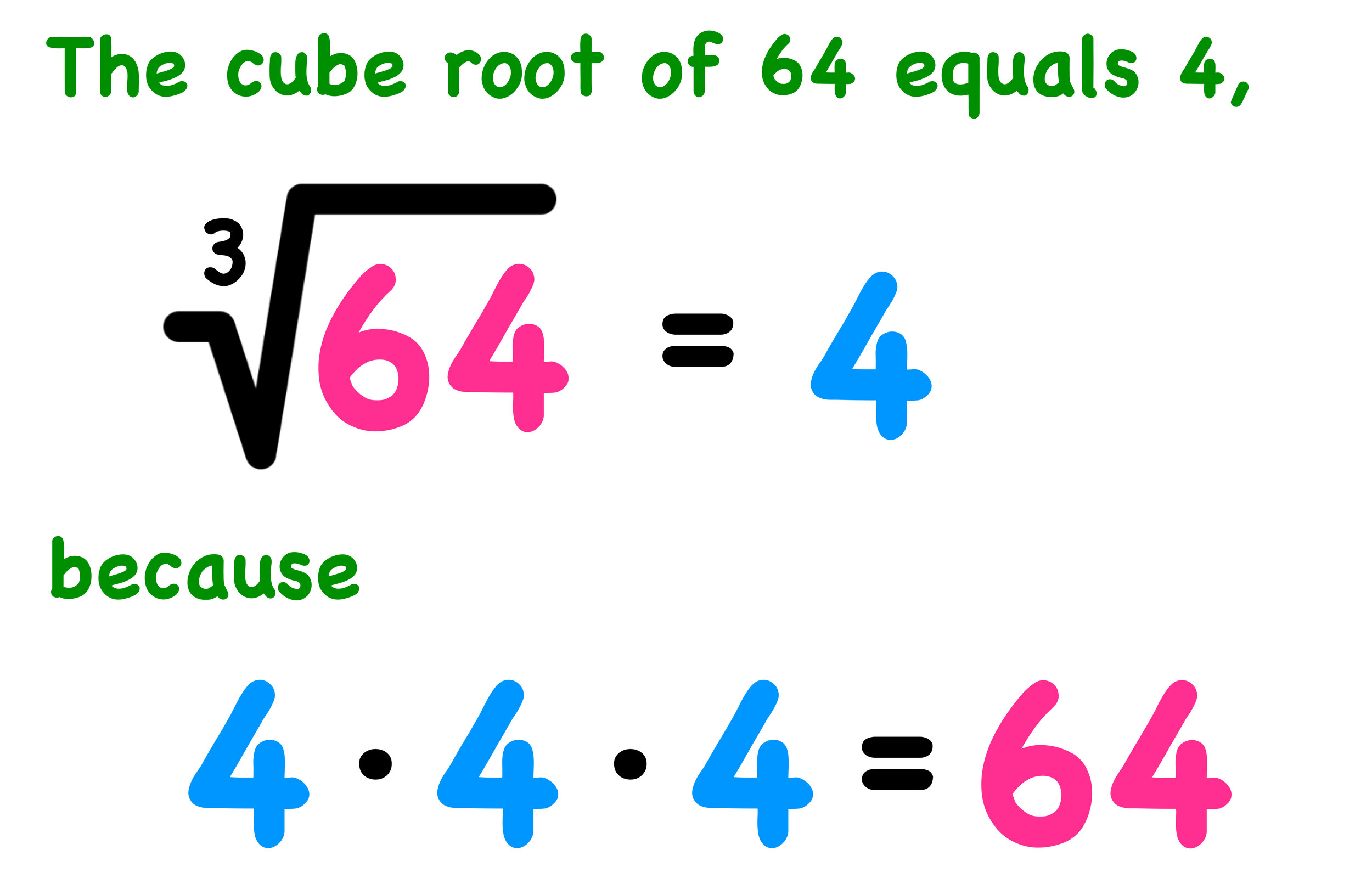
40 cubes and cube roots worksheet answers Worksheet Master

Details

Cubes, Cube roots, square and square roots A3 Poster • Teacha!

Details

Perfect Cubes and Cube Roots (solutions, examples, videos, worksheets

Details

Detail Author:

Name : Prof. Bridie Glover PhD
Username : kuhlman.jaleel
Email : dallin.king@yahoo.com
Birthdate : 1981-07-24
Address : 7751 Brando Common Terryville, MD 96114
Phone : (828) 234-2619
Company : Schuppe, Gaylord and Rosenbaum
Job : Model Maker
Bio : Quisquam consequatur ut eos facilis. Sequi ullam occaecati asperiores unde at eos. Exercitationem officia expedita vero amet architecto voluptatem molestiae architecto.

Socials

facebook:

url : https://facebook.com/ilene.lakin
username : ilene.lakin
bio : Dolore non praesentium praesentium neque. Eos quas quae dolorem.
followers : 1118
following : 29

tiktok:

url : https://tiktok.com/@ilenelakin
username : ilenelakin
bio : Et ut labore odit quia corporis voluptas. Provident quia iste nobis quia.
followers : 2966
following : 433