Understanding Graphs: A Comprehensive Guide & Resources

22 May, 2025

Can a single visual representation truly unlock the secrets hidden within complex datasets? Graphs, the unsung heroes of data visualization, possess the remarkable ability to transform bewildering information into easily digestible insights.

At its core, graphing is the art and science of creating visual representations of data using diagrams or charts. This process allows us to distill complex information, process it efficiently, and ultimately, arrive at a clearer understanding. But the realm of graphs extends far beyond simple bar charts and pie graphs. It encompasses a diverse landscape of forms, each designed to highlight specific relationships and patterns within data. Whether you're charting the trajectory of a rocket, analyzing the stock market, or understanding the growth of a population, graphs provide an indispensable toolkit for making sense of the world around us.

Graphs come in many different forms to better reflect the data they present. You can represent data in the form of a line graph, which uses dots connected by lines to show how amounts change over time. For example, a line graph could show the highest temperature for each month during one year, the bottom of the graph would show the months.

Let's take a look at the fundamental components that make up a graph. A graph is a mathematical representation composed of vertices, or nodes, connected by edges, also known as links. The vertex is an important component of a graph, also known as a node. The graph may be defined as a diagram that showcases and represents data. Through graphs, complex information can be simplified, processed, and understood in a visualized format. Graphs are essential tools for visualizing relationships between variables, making complex data more comprehensible.

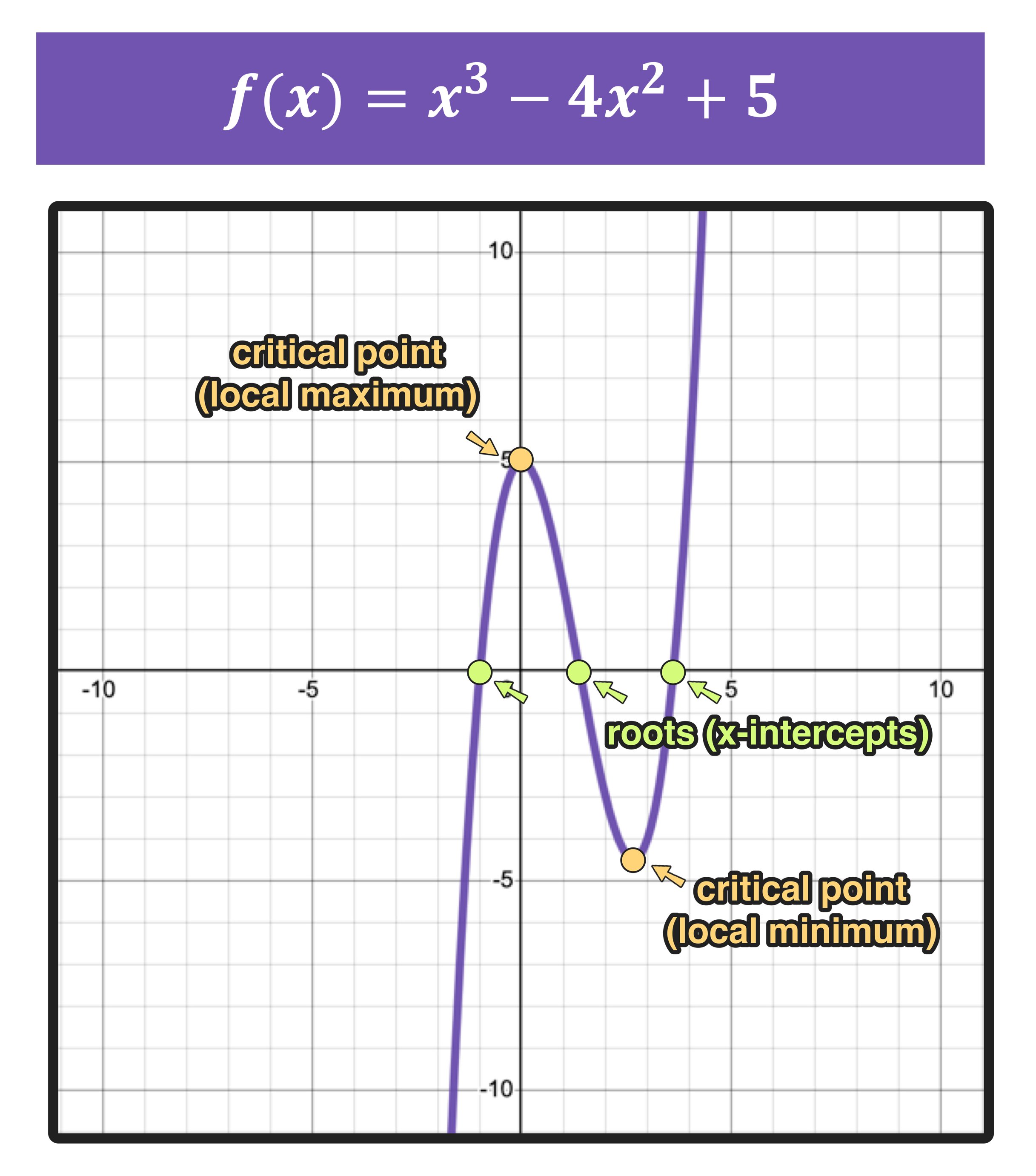
Graphing functions is the process of illustrating the graph for the function that corresponds to it, and drawing the curve of the corresponding function. Graphing basic functions like linear, quadratic, cubic, etc. is pretty simple, while graphing functions that are more complex, like rational, logarithmic, etc., requires some skill and some mathematical concepts to understand correctly. Graphing another function, like \(g(x)=x^2+1\), will show the points of intersection of the two curves. To see the points of interest, select the curve youre interested in (you can click on it on the graph or on its expression line).

Aspect	Details
Definition	Graphing, in simple terms, is the process of creating a visual representation of data using a diagram or chart.
Types of Graphs	Line graphs, Bar graphs, Pie charts, Scatter plots, and more.
Basic Components	Vertices (nodes), Edges (links).
Purpose	To visualize relationships between variables, simplify complex data, and aid in decision-making.
Applications	Data analysis, Statistics, Mathematics, Science, Finance, and various other fields.
Tools	Graphing calculators, software like Excel, GraphPad, and Origin; open-source libraries like Plotly.
Complexity	Graphing basic functions like linear, quadratic, cubic, etc. is simple. Graphing more complex functions like rational, logarithmic, etc., requires more skill and understanding of mathematical concepts.
Benefits	Helps process and make sense of large datasets, and facilitates informed future decisions.
Examples	Revenue growth over time, the relationship between temperature and ice cream sales, or the performance of different investment portfolios.
Reference	Oxford Languages

The journey through the world of graphs often begins with simple functions. Plotting functions such as linear, quadratic, and cubic equations might seem straightforward. However, the real challenge and intrigue arise when exploring the graphs of more complex functions. Those might be rational, logarithmic, and others, it demands some skill and knowledge to understand them correctly.

Think of a graph as a map. A map uses lines, symbols, and labels to help you navigate a physical space. In a similar way, a graph uses a coordinate system, data points, and lines to visualize relationships between variables. The primary purpose of disconnected graph analysis is to determine isolated subnetworks or clusters inside of a larger system.

Let's delve into some key principles that will help you better grasp graphs. One fundamental aspect is the concept of a vertex, also known as a node. This is a crucial building block. A graph, in essence, is a diagram that showcases and represents data. By using graphs, complex information is simplified, processed, and understood in a visual format. Graphs are necessary because they can help us process and make sense of voluminous data and with graphs, we can make informed future decisions.

Graphing, at its core, is about creating a visual representation of data using a diagram or chart. You can graph a quadratic equation using the function grapher, but to really understand what is going on, you can make the graph yourself.

The graph of a quadratic function is a parabola and tells the nature of the quadratic function. Plotting a quadratic equation involves plotting the data on a coordinate plane.

There are instances when graphing by hand becomes inefficient, and the method of solving by graphing is usually employed when utilizing a graphing calculator. It is also important to note that the other methods such as substitution, elimination, and row reduction are often more accurate and efficient.

Graphing calculators and software programs like Excel, GraphPad, and Origin are indispensable tools for creating and analyzing graphs. Texas Instruments has been making graphing calculators for decades, and they're still the best of the best. The graphing calculator is beneficial whether youre a student working on assignments or someone solving equations professionally. By integrating multiple features into a single device, it simplifies tasks and saves both time and effort.

The simplest quadratic equation is: \(f(x) = x^2\). Its graph is simple too: This is the curve \(f(x) = x^2\), it is a parabola. Your graph shows that the revenue your team produced during the last year steadily increaseda very encouraging trend! You decide that the graph is definitely what youll present at the meeting. A line graph uses dots connected by lines to show how amounts change over time. For example, a line graph could show the highest temperature for each month during one year. One side of the graph would show a range of temperatures. The bottom of the graph would show the months.

In this module, youll learn how to create Cartesian graphs and why graphs are an especially useful means of conveying information. A graph is a mathematical representation that consists of a set of vertices (or nodes) connected by edges (or links). In the context of data analysis and statistics, graphs are essential tools for visualizing relationships between variables, making complex data more comprehensible.

Learning how to read graphs, and perhaps even create their own graph, is one means to an end goal. Sorting and classifying data is a means of organizing important information. Graphing teaches comparison in numbers and quantities.

In this section we need to review some of the basic ideas in graphing. It is assumed that youve seen some graphing to this point and so we arent going to go into great depth here. We will only be reviewing some of the basic ideas. We will start off with the rectangular or Cartesian coordinate system.

The exploration of graphs extends beyond the classroom. Consider the application of disconnected graph analysis, which aims to identify isolated subnetworks or clusters within a larger system. These types of analyses are often used in social network analysis, biological networks, and other systems where understanding the interconnectedness of components is essential.

A graph with three vertices and three edges, or the graph in which from each node there is an edge to each other node. A graph containing at least one cycle is known as a cyclic graph. A directed graph that does not contain any cycle. Also, a graph is sometimes called an undirected graph to distinguish it from a directed graph, or a simple graph to distinguish it from a multigraph.

Whether you are a student tackling assignments or a professional solving equations, a graphing calculator can be a beneficial tool. By integrating multiple features, such as plotting graphs, visualizing algebraic equations, adding sliders, and animating graphs into a single device, it simplifies tasks and saves both time and effort.

The world of graphs offers a powerful way to extract meaning from data. By mastering the principles and tools of graphing, you can unlock a new level of understanding and make informed decisions in any field.

Details

Graphing Linear Functions Examples & Practice Expii

Details

How to Graph a Function in 3 Easy Steps — Mashup Math

Details

Detail Author:

Name : Tyrell Ruecker
Username : bergstrom.solon
Email : andy.boehm@schroeder.org
Birthdate : 1991-12-23
Address : 799 Adalberto Land Suite 158 South Haileetown, ID 57554-7303
Phone : 240-724-6470
Company : O'Keefe, Fadel and Kemmer
Job : Pewter Caster
Bio : Laboriosam quas eius pariatur placeat odit ab aspernatur. Molestiae quod mollitia et natus debitis repudiandae. Voluptates libero dolor dignissimos amet sunt praesentium.

Socials

twitter:

url : https://twitter.com/kasey_dev
username : kasey_dev
bio : Voluptas minus quisquam explicabo officia pariatur et. Sint quis suscipit autem. Labore id dolores iste aut quis laudantium similique ratione.
followers : 6624
following : 2575

linkedin:

url : https://linkedin.com/in/kub1980
username : kub1980
bio : Porro omnis cupiditate cum nulla.
followers : 3994
following : 566

facebook:

url : https://facebook.com/kubk
username : kubk
bio : Similique voluptas aliquam sed. Consequatur accusantium dolor sit distinctio.
followers : 113
following : 291