Understanding Linear Equations & Graphs: A Beginner's Guide

Is mathematics a language unto itself, capable of describing the universe with unparalleled precision? At its core, the concept of "linear" serves as a fundamental building block, forming the bedrock of countless mathematical principles and applications. Understanding linearity unlocks doors to comprehending everything from the simplest relationships to the most complex systems.

The term "linear" might seem straightforward, but its implications ripple through various branches of mathematics and beyond. It essentially describes a relationship that can be visualized as a straight line. This straight line represents a consistent, predictable relationship between variables. Whether it's a simple equation or a complex system, the essence of linearity lies in its unwavering adherence to a consistent rate of change. This makes linear models incredibly useful for predictions and understanding patterns.

Let's consider the basic definition: a linear equation is an equation where the highest power of the variable is always 1. This might seem trivial, but it's the cornerstone of the concept. When we graph this equation, it always yields a straight line. This geometrical representation is the visual manifestation of the "linear" property, a direct correlation between the equation's algebraic structure and its graphical form.

• October 17 Zodiac Uncover Love Compatibility Secrets
• Gabriel Fernandez The Trials Tragic Abuse That Shocked The World

Linearity permeates various domains, including algebra, calculus, and even fields like physics and computer science. In linear algebra, for example, the study of linear equations and their representations within vector spaces using matrices is central. Modern geometrical concepts find their foundations in this branch of mathematics. The fundamental concept of a straight line, represented by a constant slope, becomes a crucial element in understanding the behaviour of the linear graph.

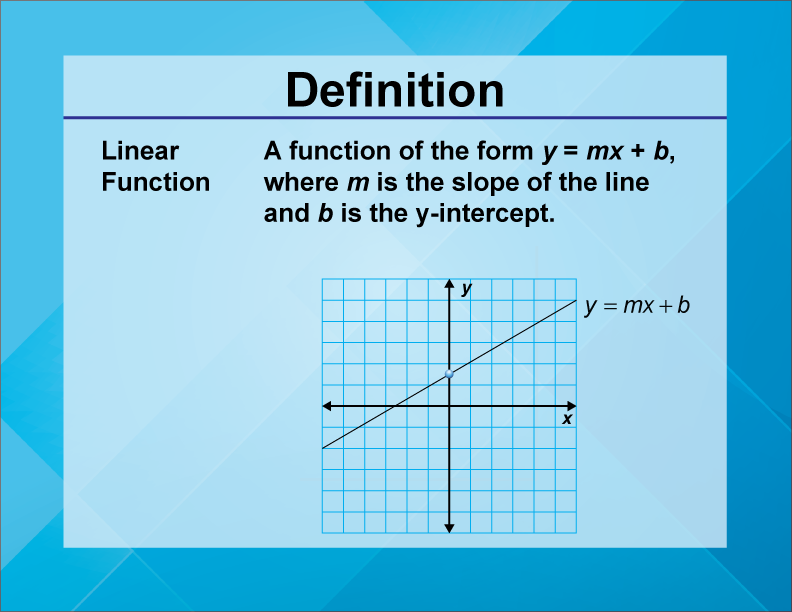
To illustrate the concept, consider the familiar linear equation form: y = mx + b. In this equation, 'm' represents the slope of the line, and 'b' is the y-intercept, the point where the line crosses the y-axis. The constant slope, the value of 'm,' dictates the line's direction and steepness. Because the slope remains constant, the graph maintains a straight line, reflecting the unchanging relationship between the variables.

It's important to acknowledge that not all relationships are linear. Nonlinear functions, as their name suggests, do not produce straight lines when graphed. They can exhibit curves, bends, and varying rates of change, making them more complex to analyze. The comparison between linear and nonlinear functions is a standard part of mathematical study, highlighting the different types of relationships that can exist.

• 1984 Events History Significance Unveiling The Year
• Emily Gold Fundraiser Tributes After Tragic Loss Support Her Family

In the realm of algebra, linearity finds its expression in the manipulation of symbols and their governing rules. The study of linear equations is a systematic theory dedicated to solving systems of these equations. They represent the mathematical relationships, allowing us to analyze the interplay between the variables in a structured way.

One can further explore linear functions. Defined as a function with one or two variables, without exponents, they also graph into a straight line. The defining aspect of such a function is the constant nature of the variables. These functions play a crucial role in mathematics, forming a foundation for various complex mathematical concepts.

Linear functions allow us to make predictions. They are essential in making predictions about the future, from predicting financial trends to understanding physical phenomena. The importance of linear functions in mathematics cannot be overstated, their predictability and simplicity make them a versatile tool for representing and analyzing the world around us.

To further delve into the nuances of linearity, let's consider the specific components that define it:

A linear equation is an algebraic equation with a degree of 1, resulting in a straight-line graph. The very word 'linear' signifies 'straight,' emphasizing the geometric representation of the relationships between variables. Linear graphs are drawn to visually represent the relationship between two quantities, offering a way to depict the relationship through a single, straight line, devoid of curves or other complex forms.

Now, let's examine the different facets of linear graphs and equations:

A linear graph is a graphical representation of a linear equation, typically with two variables, x and y, expressed in the form of a graph. Linear relationships can be expressed graphically.

In this context, the concept of linearity is related to the slope of the line, the value of "m" in the equation y = mx + b. In a linear graph, the slope is always constant, and this constant slope gives rise to a straight line. The graph doesn't necessarily go through the origin. This can be determined by the value of 'b' in the equation y = mx + b.

Linear algebra, at its core, revolves around the study of linear equations and their representations within vector spaces, primarily using matrices. This branch of mathematics is dedicated to understanding linear functions and vectors, serving as one of the most central topics in mathematics. Linear algebra underpins many modern geometrical concepts. The study of linear algebra is instrumental in solving systems of linear equations.

Here is a compilation of symbols from the different branches of algebra, including basic algebra, number theory, linear algebra, and abstract algebra.

Symbol	Name	Meaning / Definition	Example
=	Equals sign	Indicates equality between two expressions	5 + 3 = 8
+	Plus sign	Indicates addition	2 + 2 = 4
-	Minus sign	Indicates subtraction	5 - 2 = 3
or	Multiplication sign	Indicates multiplication	3 4 = 12, 3 4 = 12
/ or	Division sign	Indicates division	6 / 2 = 3, 6 2 = 3
()	Parentheses	Indicates the order of operations	(2 + 3) 4 = 20
[]	Brackets	Indicates the order of operations (used with parentheses)	[2 + (3 4)] = 14
{}	Braces	Indicates a set of numbers or elements	{1, 2, 3, 4}
x, y, z, etc.	Variables	Represent unknown values	y = 2x + 1
an	Exponent	Indicates repeated multiplication	23 = 2 2 2 = 8
	Square root	The value that, when multiplied by itself, gives the original number	9 = 3
|x|	Absolute value	The distance of a number from zero	|3| = 3
	Summation	Indicates the sum of a series of numbers	i=13 i = 1 + 2 + 3 = 6
	Integral	Represents the area under a curve	x2 dx
f(x)	Function notation	Represents a function of x	f(x) = x + 2
	Element of	Indicates that an element belongs to a set	2 {1, 2, 3}
	Not an element of	Indicates that an element does not belong to a set	4 {1, 2, 3}
	Subset of	Indicates that a set is a subset of another set	{1, 2} {1, 2, 3}
	Union	Represents the combination of elements from two or more sets	{1, 2} {2, 3} = {1, 2, 3}
	Intersection	Represents the common elements of two or more sets	{1, 2} {2, 3} = {2}
or {}	Empty set	Represents a set with no elements
	For all	Indicates that a statement is true for all elements in a set	x , x2 0
	There exists	Indicates that a statement is true for at least one element in a set	x , x + 1 = 0
	Implies	Indicates logical implication	If x = 2, then x2 = 4
	If and only if (iff)	Indicates logical equivalence	x = 2 x2 = 4
or ~	Negation	Indicates the opposite of a statement	(x = 2)
	And	Indicates that both statements are true	x > 0 y > 0
	Or	Indicates that at least one statement is true	x > 0 y > 0
p q	Implication	If p, then q	If it rains, then the ground is wet
p q	Equivalence	p if and only if q	The triangle has three sides the triangle is a polygon
p q	Conjunction	p and q are both true	The sun is shining the sky is blue
p q	Disjunction	p or q or both are true	I will eat pizza I will eat pasta
<	Less than	Indicates that a number is smaller than another	3 < 5
>	Greater than	Indicates that a number is larger than another	5 > 3
	Less than or equal to	Indicates that a number is smaller than or equal to another	3 5
	Greater than or equal to	Indicates that a number is larger than or equal to another	5 3
	Not equal to	Indicates that two expressions are not equal	5 3
	Identical to	Indicates that two expressions are identical	a a
	Approximately equal to	Indicates that two values are close to each other	3.14
	Proportional to	Indicates direct proportionality	y x
	Partial derivative	Indicates a derivative with respect to one variable	f/x
	Nabla or Del	Represents a vector differential operator	f
	Box	Used to denote the end of a proof
	Delta	Represents change	x
lim	Limit	The value that a function or sequence "approaches"	lim x2 (x+1) = 3
dx, dy	Differentials	Infinitesimal changes	dy/dx
e	Euler's number	The base of the natural logarithm	e 2.71828
i	Imaginary unit	-1	i = -1
	Pi	The ratio of a circle's circumference to its diameter	3.14159
sin, cos, tan	Trigonometric functions	Sine, cosine, tangent	sin(x), cos(x), tan(x)
log	Logarithm	The inverse function of exponentiation	log2(8) = 3
det(A) or |A|	Determinant	A scalar value that can be computed from the elements of a square matrix	det(A)
A-1	Inverse matrix	The matrix that, when multiplied by the original matrix, yields the identity matrix	A-1
AT	Transpose matrix	The matrix obtained by interchanging the rows and columns of a given matrix	AT
I	Identity matrix	A square matrix with ones on the main diagonal and zeros elsewhere
M(n, m, F)	Matrix notation	Matrices with dimensions n m over the field F
Span(S)	Span	The set of all linear combinations of the vectors in S
Ker(T)	Kernel	The set of all vectors that map to the zero vector
Im(T)	Image	The set of all possible outputs of the transformation
C(X)	Continuous functions	The set of all continuous functions
L2	Square-integrable functions	The set of all square-integrable functions

When plotting a linear sequence on a graph, the outcome is invariably a straight line. This geometrical interpretation underscores the central role of linearity in mathematics. It helps illustrate the concept of an arithmetic sequence by visualizing the pattern on a graph.

This provides us with the components to address how linear graphs are generated, including the equations behind the graph. Let's consider the equation of a linear graph. Generally, it is a linear equation with two variables, x and y, and can be written in the general form y = mx + c or y = mx + b. It also helps provide solved math problems to help you practice your learning.

A linear graph is a visual representation of a linear equation. It offers a straightforward way to represent a linear equation involving two variables, usually x and y. With a constant slope, linear graphs are easy to analyze and utilize for various mathematical applications. A deeper understanding of linearity enhances one's ability to model and analyze a wide range of phenomena.

Detail Author:

• Name : Prof. Bridie Glover PhD
• Username : kuhlman.jaleel
• Email : dallin.king@yahoo.com
• Birthdate : 1981-07-24
• Address : 7751 Brando Common Terryville, MD 96114
• Phone : (828) 234-2619
• Company : Schuppe, Gaylord and Rosenbaum
• Job : Model Maker
• Bio : Quisquam consequatur ut eos facilis. Sequi ullam occaecati asperiores unde at eos. Exercitationem officia expedita vero amet architecto voluptatem molestiae architecto.

Socials

facebook:

• url : https://facebook.com/ilene.lakin
• username : ilene.lakin
• bio : Dolore non praesentium praesentium neque. Eos quas quae dolorem.
• followers : 1118
• following : 29

tiktok:

• url : https://tiktok.com/@ilenelakin
• username : ilenelakin
• bio : Et ut labore odit quia corporis voluptas. Provident quia iste nobis quia.
• followers : 2966
• following : 433

linkedin:

• url : https://linkedin.com/in/ilene_lakin
• username : ilene_lakin
• bio : Fugiat nemo voluptas ut soluta repudiandae.
• followers : 5908
• following : 2626