Understanding Standard Form: Equations & Conversions | Math Guide

22 May, 2025

Is there a single, universally applicable way to express a linear equation? The answer, surprisingly, is no; several forms exist, each offering unique advantages depending on the task at hand, but the Standard Form consistently proves its versatility.

Consider the landscape of linear equations. Theres the slope-intercept form, a familiar friend, and the point-slope form, a handy tool for specific scenarios. Each has its own strengths and weaknesses, shaping how we understand and manipulate these fundamental mathematical structures. For example, the point-slope form shines when you have the slope and a single point, providing a direct path to the equation. Standard form, though, often takes the lead when dealing with systems of equations or specific algebraic manipulations.

Lets delve into the practical aspects of standard form, specifically examining its application and utility across varied mathematical scenarios. The beauty of standard form lies in its ability to streamline processes and offer clarity, particularly when solving systems of equations or performing other algebraic manipulations. Understanding standard form is not just about memorization; it's about gaining a strategic advantage in problem-solving.

Aspect	Details
Definition	The standard form of a linear equation in two variables is generally expressed as: Ax + By = C, where A, B, and C are integers, and X and Y are the variables.
Purpose	To provide a consistent and organized way to represent linear equations, aiding in solving and graphing.
Key Features	Variables (x and y) are on the same side of the equation. Constants are on the other side. Coefficients (A and B) are typically integers.
Advantages	Easier to align variables in systems of equations. Simplifies finding the x and y intercepts. Useful for applying the elimination method.
Disadvantages	Less intuitive for finding the slope directly. May require rearrangement to graph easily.
Applications	Solving systems of linear equations. Finding intercepts of a line. Graphing linear equations. Modeling real-world scenarios.
Conversion	Easily converted from and to slope-intercept form and point-slope form.
Examples	3x + 4y = 7 -2x + y = 5 x - 5y = 0

The standard form equation can take a variety of forms. Whether you're tackling a system of equations or simply trying to determine the intercepts of a line, standard form offers a streamlined approach. One of the immediate benefits of standard form is its utility in systems of equations. When you have a system of two or more linear equations, standard form allows for easy alignment of variables. This alignment is crucial when using methods such as elimination or substitution to solve for the unknown variables. Imagine two equations: 2x + 3y = 7 and x - y = 1. The standard form simplifies the process, making it easy to see how to combine the equations and solve for x and y.

Converting equations between different forms, such as slope-intercept and standard forms, is a fundamental skill. The ability to convert between these forms is often essential for problem-solving. Consider the slope-intercept form (y = mx + b), where 'm' is the slope, and 'b' is the y-intercept. Translating this into standard form (Ax + By = C) involves rearranging the equation to have the x and y terms on one side and the constant on the other. For instance, given y = 2x + 3, rearranging it gets us -2x + y = 3, which fits the standard format.

The manipulation of equations often requires dealing with fractions, a common hurdle in many mathematical problems. To get rid of fractions in an equation, one must multiply all terms by the least common multiple (LCM) of the denominators. This process ensures that the equation remains balanced while eliminating the need to deal with fractional coefficients. Take for instance, the equation (1/2)x + (1/3)y = 1. The LCM of 2 and 3 is 6, multiplying the entire equation by 6 yields 3x + 2y = 6, which is now free of fractions.

Scientific notation, commonly called standard form, is vital for expressing and manipulating very large or small numbers. It provides a more compact and manageable way to represent numbers that would otherwise be cumbersome to write. This form simplifies calculations and ensures clarity. For example, the speed of light, a very large number, is 2.998 x 10^8 meters per second. Using standard form, we can clearly represent such a vast quantity.

The standard form of a quadratic equation takes the format of: f(x) = ax + bx + c, where 'a' is not zero. This form is essential for identifying the characteristics of a quadratic function, such as its vertex and the direction it opens. It is a crucial step to factoring a quadratic equation to find common factors or find the roots. It is also very helpful in quadratic formula.

Understanding the nature of quadratic equations is aided by standard form. Recognizing the values of a, b, and c in this standard form is crucial for solving the equation. Factoring is the technique of breaking down polynomial expressions into their constituent factors, simplifying complex equations, and helping to identify common divisors. When you know a, b, and c in quadratic equations, this simplifies the process. By factoring and identifying coefficients, we can solve the quadratic equation.

For instance, when a quadratic equation appears as x + 6x + 8 = 0, you can easily spot that a = 1, b = 6, and c = 8. This understanding of the coefficients unlocks several problem-solving paths, from factoring to applying the quadratic formula. Its a key step to understanding and solving quadratic equations in different contexts.

Equations can be expressed in various ways, with the slope-intercept form and standard form standing out as the most prevalent. The ability to transition fluidly between these forms is a crucial skill. Starting with an equation in slope-intercept form like y = 2x + 5, we can easily move it to standard form, resulting in -2x + y = 5. This transition underlines the interconnectedness of different equation forms, as you are essentially rewriting the same relationship in different ways.

The standard form equation's format simplifies alignment and processing of variables, making it a perfect match for the elimination technique. Standard form is written as Ax + By = C and is a cornerstone of linear algebra. A clear example can be found in the pair of equations, 3x + 2y = 7 and x - y = 1. The elimination method is greatly helped by the uniform positioning of variables.

Standard form goes by the name of "general form", Ax + By + C = 0. This offers a different angle on linear equations. This form emphasizes the coefficients and constants and also the relationship between the variables and the overall equation. The equations properties can be easily examined, and it offers a different strategy for manipulation.

When we consider equations in two variables, a standard form like Ax + By = C is fundamental. In this form, 'x' and 'y' are the variables, and A, B, and C are integers. For instance, 3x + 4y = 8 is a perfect example of standard form. To work effectively, we need a basic understanding of how to write the equation.

Converting between standard form and other forms, like the point-slope form, involves moving the variables to the left side of the equation. The ability to convert is essential for manipulating an equation to solve a problem. For example, if you're given a point-slope equation, you might rearrange it into standard form to make it easier to solve using other methods.

The standard form is often the initial step when dealing with linear equations, serving as a foundational structure. This form provides a straightforward means of defining and examining the relationships in the equation.

Understanding Equation Standard Form Algebra Study

Details

Details

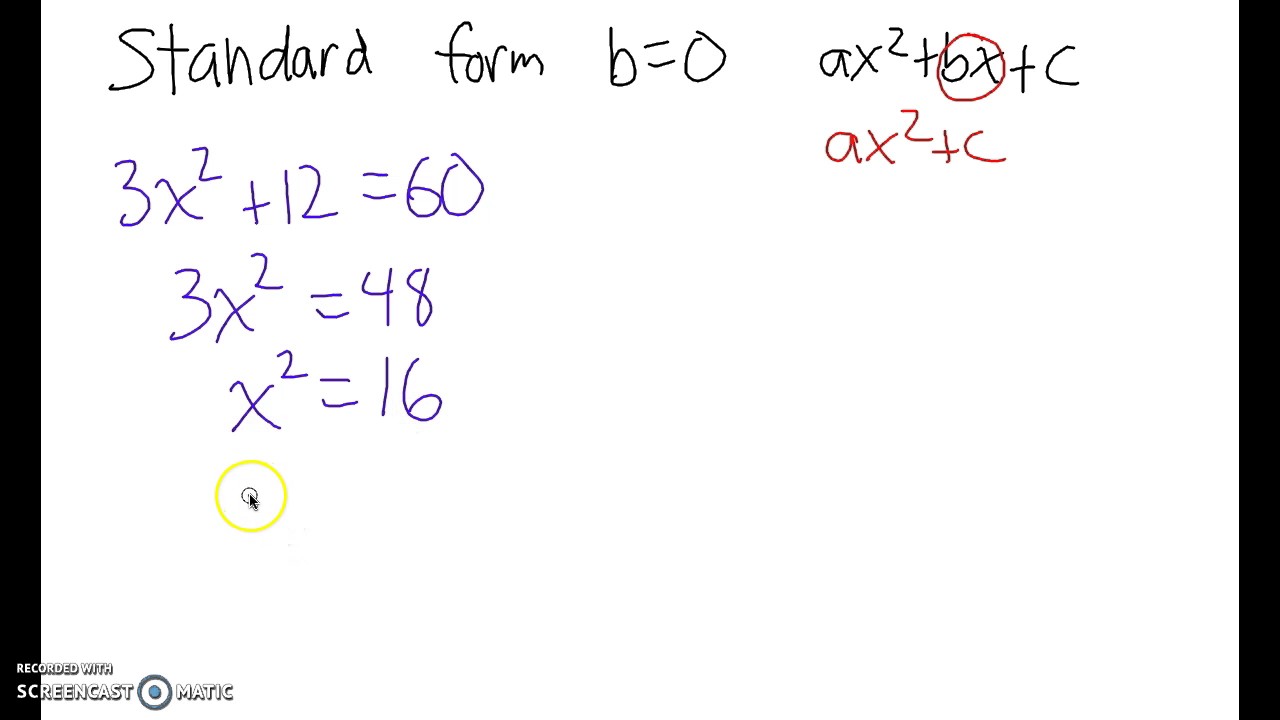
Solving a quadratic equation in standard form when b=0 YouTube

Details

Detail Author:

Name : Fannie Sawayn
Username : carmine.mcclure
Email : leffler.payton@yahoo.com
Birthdate : 2004-08-22
Address : 2108 Bergstrom Rue Port Pierce, HI 84141-7618
Phone : +1-863-969-0109
Company : Shanahan, Schiller and Reilly
Job : Farmworker
Bio : Aut possimus ea temporibus dolorum voluptatem vero voluptatum. Asperiores in aut necessitatibus perferendis et numquam. Culpa in qui reprehenderit et voluptas beatae omnis rerum.

Socials

instagram:

url : https://instagram.com/einarconn
username : einarconn
bio : Laudantium eos quia consectetur architecto. Earum ut rem illo non recusandae qui non.
followers : 5656
following : 2115

twitter:

url : https://twitter.com/conne
username : conne
bio : Id adipisci expedita aut velit. Maiores aliquam et eligendi vitae quam illum ea.
followers : 391
following : 717