Unit Rate Math: Learn & Solve Problems (Whole Numbers & More)

26 May, 2025

Can you effortlessly compare the cost of shredded cheese sold in different-sized bags, or calculate the precise medication dosage delivered through an IV drip? Mastering unit rate math is not just a classroom exercise; it's a fundamental skill that unlocks understanding in various real-world scenarios, from everyday shopping decisions to complex medical calculations.

The realm of unit rate math encompasses a broad spectrum, beginning with the fundamental concepts of ratios and proportions introduced in 6th and 7th grade. This foundational understanding extends to more intricate applications, touching on areas like calculating intravenous flow rates in healthcare settings, where precision is paramount. The core concept centers around expressing a rate as a quantity per a single unit of another quantity the "unit rate." For instance, if a car travels 150 kilometers in 3 hours, the unit rate, or the speed, is calculated as kilometers per hour (km/h). The ability to manipulate and compare these rates is crucial for problem-solving in diverse situations.

Consider the scenario of a nurse administering medication. The accurate calculation of intravenous (IV) flow rates is a critical responsibility. In this context, the unit rate is expressed as milliliters per hour (ml/hr), representing the precise amount of fluid delivered over a specific period. While modern IV pumps often automate this process, the underlying principles remain essential for understanding and ensuring patient safety. Proficiency in unit rate math allows healthcare professionals to verify pump settings, troubleshoot potential issues, and make informed decisions based on the patient's needs.

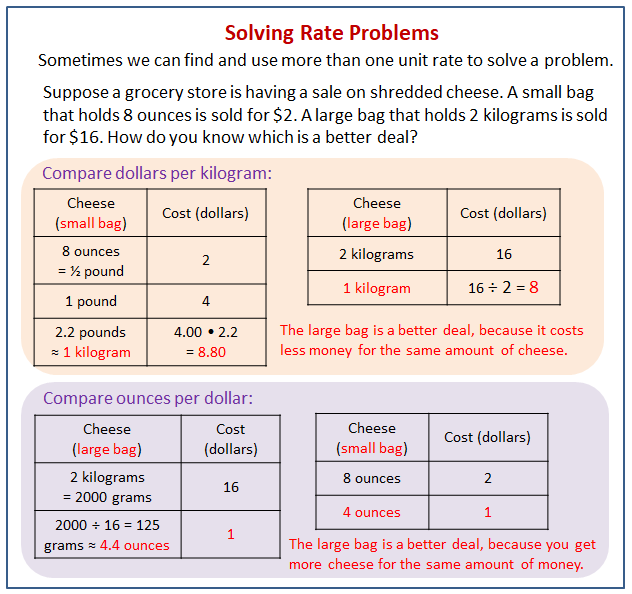
Beyond the medical field, the principles of unit rate extend to the realm of practical decision-making. When faced with a sale on shredded cheese, the ability to determine the best deal requires calculating the unit price the cost per ounce or per kilogram. By comparing unit prices, consumers can make informed choices, maximizing their purchasing power. Similarly, in situations involving speed, distance, and time, the ability to calculate the unit rate (speed) enables one to determine travel times, plan routes, and assess performance.

Rate problems are frequently encountered in various mathematical contexts. Speed, distance, and time problems are a standard application of linear equations. When solving these problems, the fundamental relationship of rate (speed or velocity) multiplied by time equals distance ([latex]r\cdot t=d[\/latex]) must be remembered. Let's say a person travels at 30 km/h for 4 hours. Knowing this, we can use the relationship rate (30 km/h) times time (4h) to compute the distance (120 km).

The core principle of unit rate involves simplifying a rate so that the denominator is 1. This facilitates straightforward comparisons. For instance, if a man covers 3 km in 30 minutes, the unit rate is calculated by dividing the distance by the time, resulting in a rate of 0.1 km per minute, or 6 km per hour. This allows for easy comparison with other rates expressed in the same units. For instance, a rate that was 20 mph higher than John's could be compared once you understand how to calculate the unit rate. Let's use this information: If Peter traveled the same distance in 2 hours, then find the distance between the two cities. If x is John's rate, then Peter's is x+20. The rate Peter travels will be higher, this means we can find the distance by calculating the rate and multiply it by time.

Often we encounter combined labor problems or work problems. These problems are a type of math problems involving rational equations. These types of problems use unit rates, combine them, and then set them equal to a defined quantity. For example, if Felicia takes 4 hours to paint a room and her daughter Katy takes 12 hours to paint the same room, then working together, they could paint the room in 3 hours. In these types of problems, we add the reciprocal of the total of time to find the total amount of work.

The concept of rates extends beyond simple calculations. In scenarios involving melting ice or changing areas, the rate of change can be applied to understand how a specific quantity is changing over time. For instance, if the area of a sheet of ice is decreasing at a rate of 0.5 m/sec, the rate at which the radius is decreasing can be calculated, given the current area. This demonstrates the adaptability of unit rate principles in dynamic situations. In real life, an understanding of rates is valuable for several scenarios. For example: A thin sheet of ice is in the form of a circle. If the ice is melting in such a way that the area of the sheet is decreasing at a rate of 0.5 m/sec, at what rate is the radius decreasing when the area of the sheet is 12 m?

The ability to solve various problems involving rates involves a few steps. First you will need to identify what you are trying to find. This will help guide you when solving the problem, and setting up the problem. Next, identify what information you have in order to solve the problem. Once you understand the information, solve the problem. Using this framework, you should be able to use rates in almost any type of mathematical context.

Ratio and Rate Word Problems, Free PDF Download Learn Bright

Details

Details

Detail Author:

Name : Dr. Piper Ziemann II
Username : qblock
Email : justice38@hotmail.com
Birthdate : 1983-07-16
Address : 3516 Schiller Roads Apt. 773 Port Stuartberg, MO 40755
Phone : +12085122065
Company : Kemmer and Sons
Job : Marine Architect
Bio : Porro quia et cum expedita omnis commodi. Rerum quia quidem dicta maxime. Veniam ipsa quis consequuntur aut. Voluptas quidem assumenda quis accusamus nihil non dolor.

Socials

linkedin:

url : https://linkedin.com/in/garrett_borer
username : garrett_borer
bio : Qui quibusdam assumenda magni explicabo.
followers : 6420
following : 2206

tiktok:

url : https://tiktok.com/@gborer
username : gborer
bio : Aut ut quisquam deleniti et.
followers : 4276
following : 2248

instagram:

url : https://instagram.com/borerg
username : borerg
bio : Cumque unde quaerat quis et. Non at sit beatae. Eum voluptate dolorum in et numquam a.
followers : 3170
following : 1586

twitter:

url : https://twitter.com/gborer
username : gborer
bio : Quos id alias voluptatum assumenda. Aut nesciunt cum ut magnam nemo nihil. Iusto odit voluptate ut repellendus doloribus.
followers : 4256
following : 758