Cube Root Explained: Concepts, Formulas, And Examples | Learn Now!

23 May, 2025

What exactly is a cube root? In essence, a cube root unravels the process of cubing a number, serving as the mathematical inverse and revealing the original value that, when multiplied by itself three times, produces a given result. This fundamental concept underpins a wide range of scientific and engineering applications, making it crucial for any student of mathematics.

The cube root of 0 is, quite simply, 0. This might seem deceptively straightforward, but it stems from the very definition of a cube root. The cube root operation asks us what number, when cubed (raised to the power of 3), gives us the original number. In the case of zero, zero multiplied by itself three times (0 0 0) equals zero. Therefore, the cube root of 0 is 0. Understanding this foundational principle is key to grasping more complex cube root calculations. The symbol used to represent a cube root is ∛ (the radical symbol) with a small "3" above it, indicating the cube root: ∛3. So, the cube root of 0 is written as ∛30 = 0.

Let's delve into the formal mathematical definition. The cube root, denoted by the radical symbol with an index of 3, is the inverse operation of cubing. Essentially, it's asking "What number, when multiplied by itself three times, results in the given number?" Mathematically, if we say that the cube root of a number 'x' is 'y', we express this as: ∛3x = y. This is equivalent to saying y3 = x. Therefore, if you know 'x', the cube root operation helps you find the value of 'y'.

Working with cube roots can be surprisingly simple in some cases and more complex in others. Perfect cubes, such as 8 (2 x 2 x 2 = 8) and 27 (3 x 3 x 3 = 27), are readily solved. However, finding the cube root of non-perfect cubes often requires approximation methods or calculators. For instance, the cube root of 10 is approximately 2.154435.

Cube roots extend beyond positive numbers. The cube root of a negative integer always results in a negative number. This is because a negative number multiplied by itself an odd number of times (like three) will always result in a negative number. For example, the cube root of -8 is -2, because (-2) (-2) (-2) = -8. This is a significant difference from square roots, which do not have real number solutions for negative numbers.

Let's examine some practical examples. We know that ∛38 = 2, because 2 2 2 = 8. Similarly, ∛327 = 3, and ∛364 = 4. The cube root of 1 is 1, as 1 1 1 = 1. These are all perfect cubes, making the solutions integers. Finding cube roots of numbers that are not perfect cubes require more advanced tools.

Consider the cube root of 30. We can estimate this value. We know that 3 3 3 = 27 and 4 4 4 = 64. Therefore, the cube root of 30 must be between 3 and 4. Using a calculator gives us a more precise value: ∛330 3.1072. This illustrates how cube root problems often require approximation.

Cube roots can be expressed using exponents. The cube root of a number 'x' is equivalent to 'x' raised to the power of 1/3. So, ∛3x = x1/3. This offers another way to understand and calculate cube roots. It highlights the inverse relationship between cubing and taking the cube root. This is a fundamental concept in mathematics.

The cube root of 0.4 can be found using a calculator. The cube root symbol is ∛3, and it applies to 0.4, as you would express it, ∛30.4. The number under the radical symbol (the 0.4 in this case) is called the radicand. Understanding this nomenclature is necessary. Using a calculator, ∛30.4 0.7368.

Similarly, finding the cube root of 0.07 involves the same principles. You are essentially trying to find the number which, when multiplied by itself three times, produces 0.07. The cube root of 0.07 is written as ∛30.07. Using a calculator, ∛30.07 0.4121.

Let's explore a few other examples. The cube root of 0.3 is the number which, when cubed, results in 0.3, written as ∛30.3. Using a calculator, the result is approximately 0.6694.

Practical applications of cube roots are wide-ranging. They appear in physics (calculating the volume of a sphere), engineering (designing three-dimensional objects), and even in financial modeling. Understanding this concept is critical in a variety of STEM (Science, Technology, Engineering, and Mathematics) fields.

Another practical example lies in calculating the cube root of 0.001331. The cube root of 0.001331 is 0.11. This result can be verified by multiplying 0.11 by itself three times: 0.11 0.11 0.11 = 0.001331.

For the cube root of 0.000512, the result is 0.08. Which is derived by the same principles as the examples above, and can be confirmed with the formula: 0.08 0.08 0.08 = 0.000512

The cube root of a number can also be found by using a prime factorization method, though this method is best for perfect cubes. Additionally, specialized calculators can be used, which will take the number, then solve to show the results in the display.

The cube of a number is the number multiplied by itself three times. The cube root is the operation to find the number. This highlights the complementary nature of the two operations.

To use a cube root calculator, enter the value inside the cube root symbol in the input field and click the "solve" button. The result will be displayed.

Here's a table providing quick facts about cube roots:

Concept	Description	Example
Definition	The inverse operation of cubing a number; finding a value that, when multiplied by itself three times, gives the original number.	The cube root of 8 is 2 (2 x 2 x 2 = 8)
Symbol	∛3 (radical symbol with index of 3)	∛327
Relationship to Exponents	The cube root of x is the same as x raised to the power of 1/3	∛3x = x^(1/3)
Cube Root of 0	The cube root of 0 is 0	∛30 = 0
Cube Roots of Negative Numbers	Cube roots can be calculated for negative numbers, and the result will also be negative.	∛3-27 = -3
Calculation Methods	Prime factorization (for perfect cubes), approximation methods, calculators.	For ∛310 (calculator use is usually necessary).
Applications	Volume calculations, 3D modeling, physics, engineering, financial modeling.	Calculating the volume of a sphere.

For further reading, please check this source: MathsIsFun.com

What is cube root? Definition with Examples Teachoo Cube Root

Details

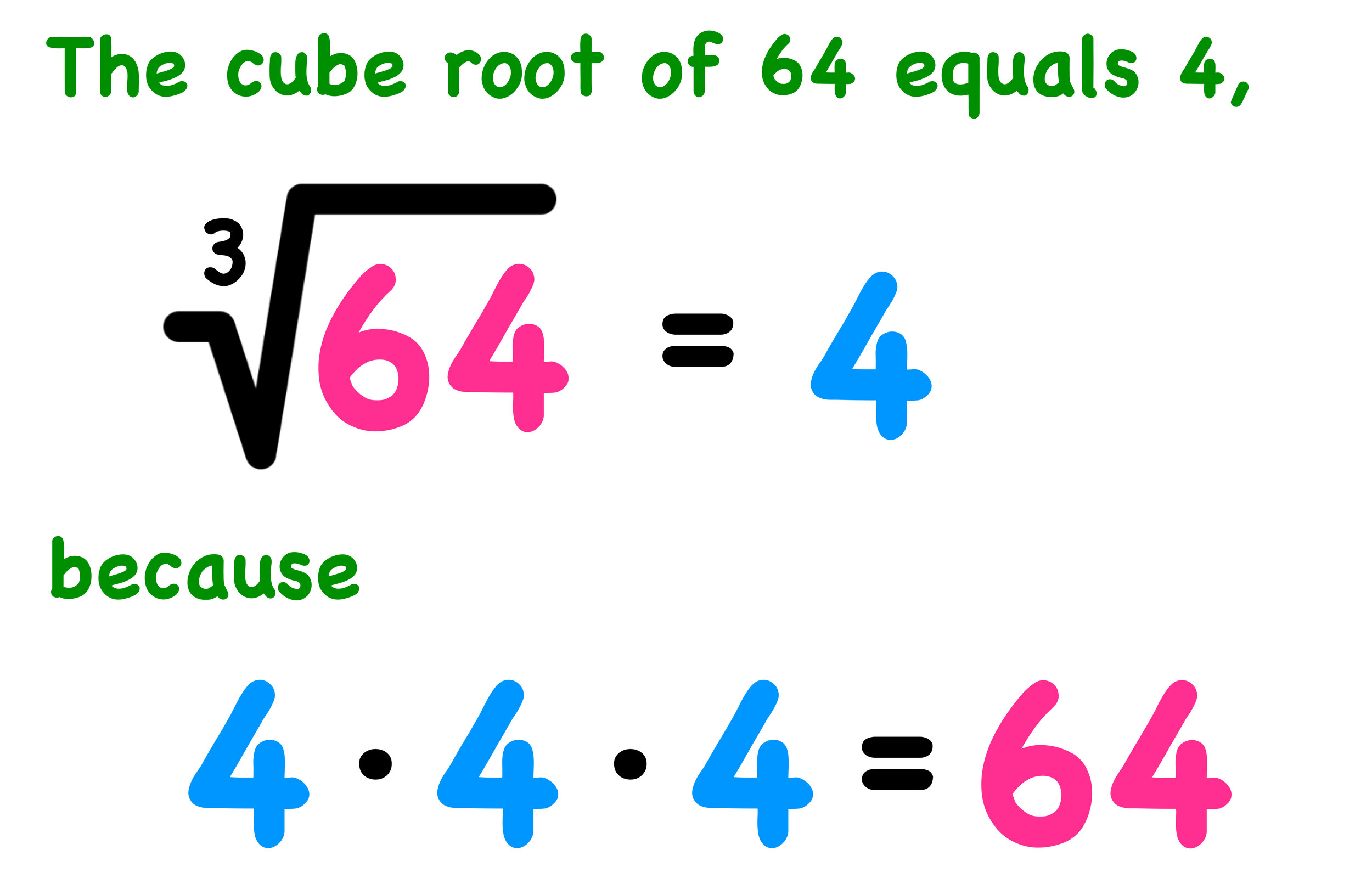
40 cubes and cube roots worksheet answers Worksheet Master

Details

Cube Root Formula and Examples (Cubes and Cube Roots)

Details

Detail Author:

Name : Yessenia Kirlin
Username : knikolaus
Email : fletcher.nicolas@yahoo.com
Birthdate : 1973-08-28
Address : 1258 Schowalter Crest Suite 378 Lake Stanton, KS 34508
Phone : +17694846339
Company : Littel PLC
Job : Fabric Mender
Bio : Non rerum distinctio amet libero est quia. Dicta vero perspiciatis eveniet eum asperiores. Adipisci eos id corporis excepturi consequatur odit. Et adipisci quia minus ipsam.

Socials

facebook:

url : https://facebook.com/ckub
username : ckub
bio : Nemo corrupti ut fuga commodi.
followers : 1125
following : 947

instagram:

url : https://instagram.com/chet_kub
username : chet_kub
bio : Ex quasi eum qui libero similique iste. Cumque distinctio delectus nulla voluptas non.
followers : 2593
following : 2738

tiktok:

url : https://tiktok.com/@kubc
username : kubc
bio : Facilis eligendi et quod odio. Quisquam dolorum atque dolor nihil.
followers : 6498
following : 2079

twitter:

url : https://twitter.com/chet.kub
username : chet.kub
bio : Tempora soluta est delectus facere nam. Et ut blanditiis eum nesciunt corrupti qui deserunt. Sed id qui enim cupiditate pariatur.
followers : 5908
following : 889