Exploring Function Graphs & Analysis: Insights & Tips [Guide]

21 May, 2025

Can understanding graphs unlock the secrets hidden within complex mathematical functions? The ability to analyze and interpret graphs is fundamental to grasping the behavior of functions, providing insights that numerical data alone cannot reveal.

Often, we are presented with data or equations, and the challenge lies in making sense of them. Graphs provide a visual language, a means of communication that translates abstract mathematical concepts into tangible forms. Whether it's understanding the trajectory of a projectile, modeling population growth, or analyzing the fluctuations of a stock market, graphs offer an accessible and powerful tool for exploration and understanding.

Analyzing a graph is not merely about reading coordinates; it is a process of decoding the narrative that the function tells. This involves identifying key features, such as intercepts, turning points, intervals of increase and decrease, and asymptotes. Each of these elements contributes to a comprehensive understanding of the function's behavior.

Consider the task of analyzing the graph of a function. We might be presented with a curve, a set of coordinates, or an equation. Our first instinct might be to reach for a graphing calculator, but the true power of analysis lies in the ability to understand the underlying principles that govern the graph's shape. This includes understanding the transformations applied to a parent function, such as shifts, stretches, and reflections.

For instance, the cube root function, a fundamental mathematical entity, can be analyzed to determine the transformations of its parent function. This involves identifying the values of a, h, and k in the general equation, which represent the vertical stretch or compression, the horizontal shift, and the vertical shift, respectively.

Constructing and analyzing the graph of an exponential function provides another layer of understanding. Exponential functions are powerful tools for modeling real-world phenomena, such as population growth, radioactive decay, or compound interest. By comparing exponential functions with linear and quadratic functions, we gain a deeper appreciation for their unique properties and applications.

Using function notation, we can build and evaluate exponential functions for various inputs. The value of 'k' in a sine graph, for example, represents the vertical shift, which affects the graph's position on the coordinate plane. In conclusion, the analysis of a graph yields valuable insights into the function's behavior, providing a comprehensive understanding of its properties.

Analyzing a function involves more than just plotting points; it requires a deep understanding of its derivatives. By employing the tools of calculus, we can identify critical points, intervals of concavity, and other key features that shape the graph. This analytical approach allows us to draw accurate and informative graphs of a wide variety of functions, from algebraic to transcendental ones.

A function's representation is often revealed through its graph. Let us consider a function that can represent the depth of snow after a snowstorm. The function f(n + 1) = f(n) + 0.8, where f(0) = 2.5, offers a view of a natural phenomenon. This equation allows us to forecast the depth of snow at any given point in time. It's a simple yet powerful model.

When we plot coordinate pairs and draw a line through the points, the result of a linear function will be a straight line. The downward slant of the graph indicates a negative slope, meaning as the input variable increases, the function's value decreases. Its the core of understanding the relationship between two variables.

Given information on key properties, we can sketch the graph. These properties are not always directly presented; we must determine them from available data. This process is fundamental to the analytical approach. The ability to analyze key properties enhances our ability to sketch and understand function representations.

Understanding function transformations is critical for interpreting graphs. Applying our knowledge, we can effectively analyze the graph of the function f(x) = (0.5)^x - 5 + 8. Plotting this, as well as its parent function, y = 0.5^x, on the same axes, allows us to visualize the transformations. This analysis also reveals that the parent function y = 0.5^x is decreasing across its domain because its base, b, is such that 0 < b < 1. The function f shifts the parent function by specific values. It is important to learn and visualize the shift.

Graphing calculators become powerful instruments to examine the intricacies of function behavior. By graphing each function, we can analyze them to ascertain whether they are even, odd, or neither. Depending on the type, we describe symmetry and interpret the properties.

Precalculus functions and graphs often center on the analysis of exponential decay functions. Understanding these types of functions is critical for modeling scenarios where quantities decrease over time, such as the decline of a radioactive substance. The initial value, the starting point of the function, is a crucial parameter, denoted by 'a' in the function's general form. The base, or rate of change, reflects how quickly the quantity diminishes.

Consider sketching the graph of a continuous function, y = f(x), decreasing on the interval (1, 1), that has a relative minimum at x = 1 and has no endpoints. In this scenario, the key properties play a critical role in constructing the graph. Understanding these aspects helps in forming accurate and meaningful representations of a function.

To understand where a function f(x) is negative, start with the provided information. If f(x) < 0 over the interval (-\u221e, -3), we can determine a second interval. Analyzing intervals and key features allows us to identify characteristics. This includes zeros, intervals of increase and decrease, and points of inflection.

The graph of the function f(x) offers another dimension. Analyzing this, we can find local minimums and maximums for the given function. These locations are critical in understanding a functions behavior.

To analyze the key features of a rational function f(x), we must follow a methodical approach. The parent function for a rational function is typically expressed as f(x) = p(x)/q(x), where both p(x) and q(x) are polynomials. Common examples include f(x) = 1/x or f(x) = (x - 1)/x². This analytical method allows for a better understanding of rational functions.

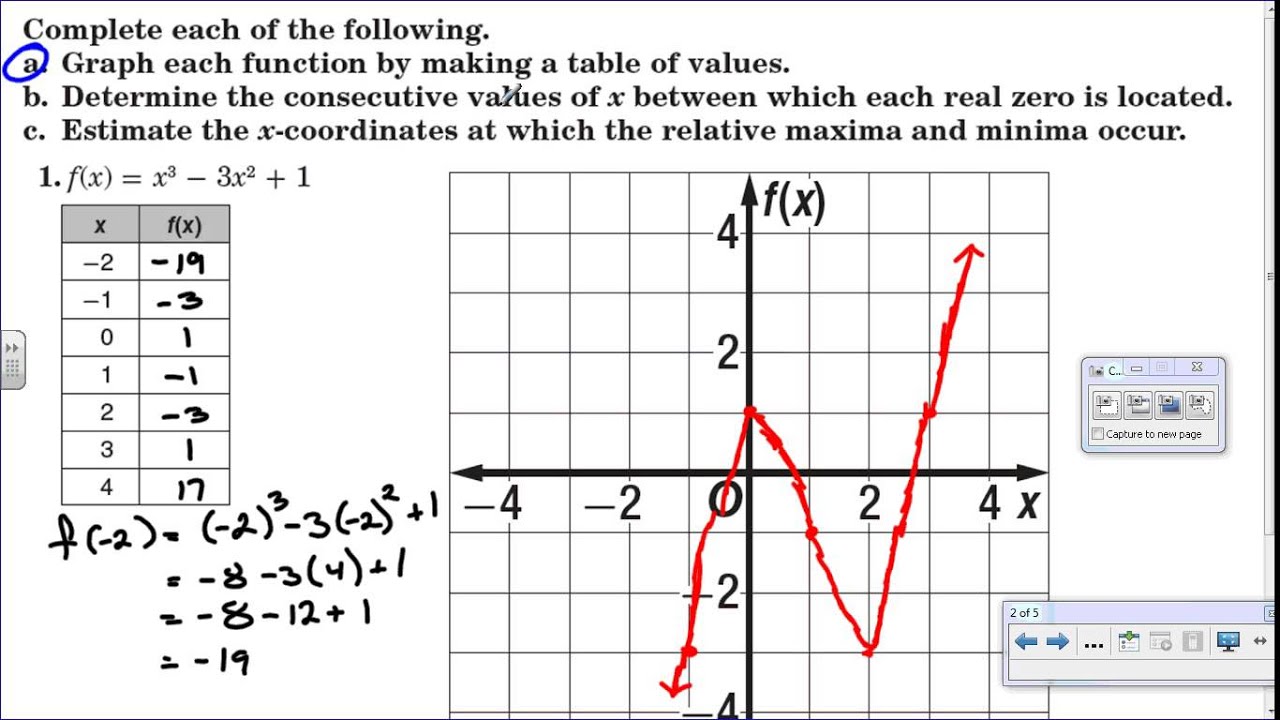
Graphing a function visually illustrates the behavior of mathematical expressions. Analyzing graphs involves identifying zeros, increases, and decreases. Locating these points leads to an understanding of how the function transforms across its domain.

This calculator can graph polynomial functions. The key to understanding the end behavior of a graph lies in analyzing its large values. The graph behaves like y = f for large values of |x|, providing insights.

The fundamental ability to analyze function graphs is an invaluable tool. Each component, from identifying transformations to assessing end behavior, enhances our capacity to interpret the complex landscape of mathematics. Whether it's solving a practical problem or exploring the depths of mathematical concepts, the ability to analyze graphs is an essential skill.

The ability to analyze graphs extends beyond pure mathematics, offering practical applications in numerous fields. The understanding of functions serves as a bridge between theoretical concepts and real-world problems.

The ability to interpret mathematical functions, model real-world situations, and predict future behaviors depends on the skills of analyzing and understanding graphs. The skills of function analysis are important.

Details

Algebra 2 Lesson 5 4 Analyzing Graphs of Polynomial Functions YouTube

Details

Precalc 1.5 Analyzing Graphs of Functions YouTube

Details

Detail Author:

Name : Ms. Marta Halvorson I
Username : andy83
Email : tyree.eichmann@hotmail.com
Birthdate : 1996-09-21
Address : 898 Franecki Row Apt. 560 Peggieborough, HI 86327-5362
Phone : +18164330273
Company : Purdy PLC
Job : Product Safety Engineer
Bio : Rerum voluptatem est dolore ut voluptas quaerat unde. Qui ut qui voluptatibus voluptatibus. Aliquam et distinctio eos accusamus. Velit necessitatibus corrupti perferendis est laudantium.

Socials

twitter:

url : https://twitter.com/bergeb
username : bergeb
bio : Quibusdam et suscipit ipsum et sint dicta cupiditate. Aut voluptas fugiat quasi voluptatem iste nam. Doloremque architecto sit esse. In modi ut quisquam quis.
followers : 2958
following : 578

linkedin:

url : https://linkedin.com/in/bergeb
username : bergeb
bio : Earum corrupti et non quis porro minus.
followers : 4183
following : 185

tiktok:

url : https://tiktok.com/@billie.berge
username : billie.berge
bio : Facere consequatur omnis reiciendis odit et quibusdam reiciendis.
followers : 5086
following : 622

facebook:

url : https://facebook.com/billie_xx
username : billie_xx
bio : Veniam autem non quidem qui quo et autem. Harum aut nam nihil ut nemo.
followers : 2223
following : 2925