Factoring Quadratic Equations: Your Step-by-Step Guide

25 May, 2025

Can unraveling the mysteries of quadratic equations truly simplify the world of algebra? Solving these equations, a cornerstone of mathematical understanding, empowers us to dissect complex problems and build a robust foundation in mathematical reasoning.

Our journey into the realm of algebra begins with the fundamental goal of mastering equation-solving. We've navigated the familiar terrain of linear equations, equations of degree 1, and now, we turn our attention to a technique for tackling certain equations of degree 2. This new landscape is populated by quadratic equations, polynomials of the second degree, where the highest power of the variable is two.

Before diving deeper, let's establish a common understanding. A quadratic equation is formally defined as an equation that can be written in the form \(ax^2 + bx + c = 0\), where 'a' is not equal to zero, and a, b, and c are real numbers. This is the standard form, the bedrock upon which we'll build our factoring approach.

The approach is not unlike solving those linear equations, but this time, our goal is to find the two roots that make the equation's statement true. In order to solve by factoring, the quadratic expression must equal zero.

In essence, our primary objective is to transform the equation into a factored form that reveals these elusive solutions. This method leans heavily on the zero product rule: if the product of two or more factors equals zero, then at least one of the factors must be zero. Consider an equation such as \(x^2 + 5x + 4 = 0\). We need to find two numbers which, when added, equal 5, and when multiplied, equal 4. The numbers 1 and 4 fit this bill, so the expression can be factored as follows:

To solve quadratic equations by factoring, a key method is utilizing what is known as the zero product property. When multiplying factors to arrive at an answer of zero, at least one of the factors must be zero.

We have to transform the equation to ensure one side of it is zero, otherwise the zero product property would be useless in solving the problem.

Solving quadratic equations using factoring involves several key steps, which we will explore in detail later. This is the most straightforward and time saving method of solving a quadratic equation as long as the binomial or trinomial is easily factorable. But be prepared, there are more than one way of solving quadratic equations, if factoring seems difficult, you can also use the quadratic formula or completing the square methods.

There is a lot of work to be done, however, a helpful calculator provides a detailed explanation on how to solve an equation.

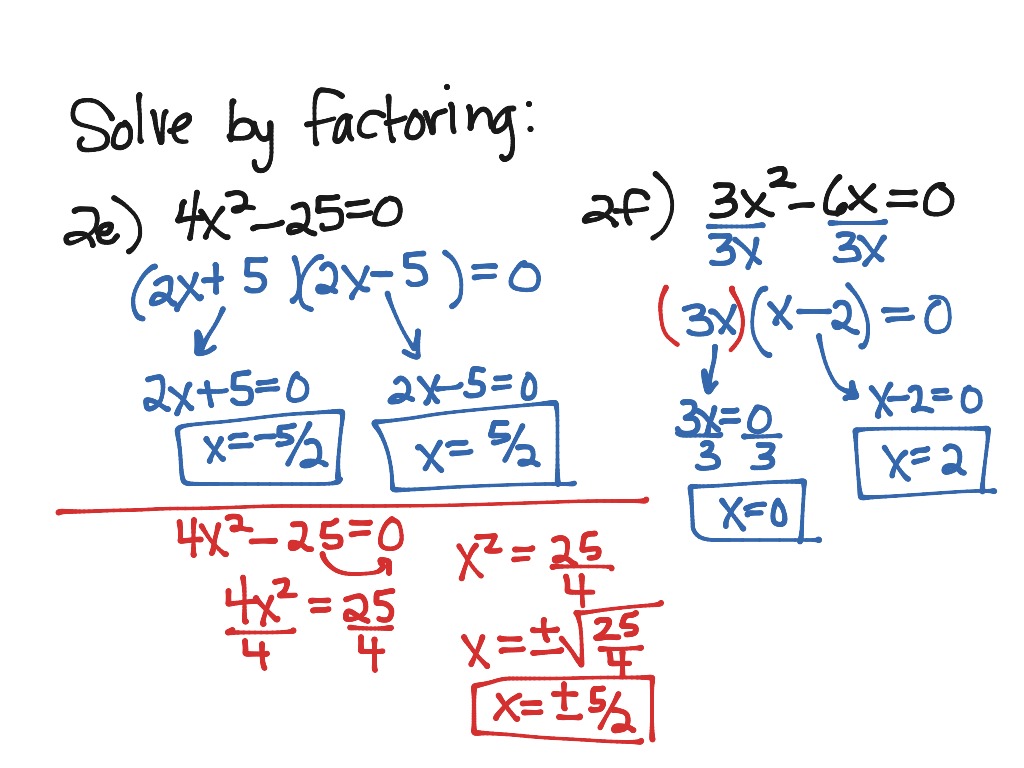
Consider the equation \(x^2 - 9 = 0\). This falls into a special case, the difference of squares, which has the form \(a^2 - b^2\). This equation can be readily factored as: \((x + 3)(x - 3) = 0\). This shows that one side is the quadratic equation, while the other is zero.

Let's delve into a practical example: factorizing \(x^2 - 9 = 0\). We're presented with a classic instance of the difference of squares. This type of factoring is readily recognizable and simplifies the equation. We know the factors must be \((x + 3)\) and \((x - 3)\). The equation can be written as: \((x + 3)(x - 3) = 0\).

To fully grasp the essence of solving by factoring, lets outline the general process. First, ensure the equation is in standard form, with all terms on one side and zero on the other. Then, factor the quadratic expression, identifying the factors. Finally, set each factor equal to zero and solve the resulting linear equations.

But remember, not every quadratic equation is easily factorable. In such scenarios, alternative methods, such as completing the square or using the quadratic formula, become essential tools in your algebraic toolkit. Consider the equation \(x^3 - x^2 - 5 = 0\). This is not a quadratic equation because of the \(x^3\) term. This can't be solved using the factoring method.

The information presented here is a refresher of these factoring skills, as they pertain to quadratic equations. Also, the degree of quadratic equation is 2, and it contains two roots. All quadratic equations have 2 solutions. However, not all quadratic equations have real number solutions. In some cases, the solutions may be complex numbers.

Factorization of quadratic equations can be done in different methods. Many online tools and calculators are available to help solve quadratic equations and break down the process step-by-step.

For instance, the factoring calculator transforms complex expressions into a product of simpler factors, while other calculators solve the equation using three different methods: the quadratic formula method, completing the square, and the factoring method. The calculator shows all the work and provides detailed explanations of how to solve an equation.

Solving equations by factoring hinges on a simple, yet powerful principle: the zero-product property. If the product of two factors is zero, then at least one of the factors must be zero. This rule is the cornerstone of our factoring strategy. This fact is called the zero factor property or zero factor principle. As the heading suggests we will be solving quadratic equations here by factoring them.

In general, we use these steps to solve a quadratic equation using the factoring method. If \(ax^2 + bx + c = 0\) is a quadratic equation, then the first step is to check if the left-hand side (LHS) is factorable. If so, then factor the LHS to get \( (px+q) (rx+s) = 0\). Then, use the zero product property and solve the equation using \( px+q = 0 \) and \( rx+s = 0\).

Remember, an equation can be written in the form \(ax^2 + bx + c = 0\) is called a quadratic equation. You can solve a quadratic equation using the rules of algebra, applying factoring techniques where necessary, and by using the principle of zero products.

When solving linear equations such as \(2x + 5 = 21\), we can solve for the variable directly by subtracting 5 and dividing by 2. However, the process is different when facing quadratic equations. These equations, characterized by the presence of an \(x^2\) term, require a more nuanced approach. The factoring method is a powerful technique to address such complexity.

By learning this technique, you're not just memorizing steps; you're building the problem solving skill that's a cornerstone of mathematical understanding.

Details

Details

Detail Author:

Name : Yessenia Kirlin
Username : knikolaus
Email : fletcher.nicolas@yahoo.com
Birthdate : 1973-08-28
Address : 1258 Schowalter Crest Suite 378 Lake Stanton, KS 34508
Phone : +17694846339
Company : Littel PLC
Job : Fabric Mender
Bio : Non rerum distinctio amet libero est quia. Dicta vero perspiciatis eveniet eum asperiores. Adipisci eos id corporis excepturi consequatur odit. Et adipisci quia minus ipsam.

Socials

facebook:

url : https://facebook.com/ckub
username : ckub
bio : Nemo corrupti ut fuga commodi.
followers : 1125
following : 947

instagram:

url : https://instagram.com/chet_kub
username : chet_kub
bio : Ex quasi eum qui libero similique iste. Cumque distinctio delectus nulla voluptas non.
followers : 2593
following : 2738

tiktok:

url : https://tiktok.com/@kubc
username : kubc
bio : Facilis eligendi et quod odio. Quisquam dolorum atque dolor nihil.
followers : 6498
following : 2079

twitter:

url : https://twitter.com/chet.kub
username : chet.kub
bio : Tempora soluta est delectus facere nam. Et ut blanditiis eum nesciunt corrupti qui deserunt. Sed id qui enim cupiditate pariatur.
followers : 5908
following : 889