Mastering Linear Equations: A Guide To Graphing & Solving Systems

22 May, 2025

Can the intricacies of the mathematical world be unveiled through the simple stroke of a pen and the strategic placement of points? Indeed, the seemingly abstract realm of linear equations offers a surprisingly accessible pathway to understanding relationships and predicting outcomes, all visualized through the elegance of a straight line.

At the heart of this exploration lies the concept of graphing linear functions. These functions, when plotted on a coordinate plane, invariably manifest as straight lines hence the term "linear." But the beauty of this simplicity belies the power within. Graphing linear equations provides a visual language, allowing us to decipher relationships between variables, anticipate trends, and solve complex problems with surprising ease. It's a skill that empowers us to move beyond abstract equations and into a world where mathematical concepts come alive, painted on the canvas of the Cartesian plane.

The core functionality of this concept lies in its ability to visually represent the relationship between variables, allowing for easier comparison and analysis. A linear equation, in its most basic form, describes a straight line, and the graph of a linear equation is a set of points in the coordinate plane that are all solutions to the equation. This is why it is referred to as "linear". If you know an equation is linear, you can graph it by finding any two solutions (x1, y1) and (x2, y2) and plotting them on a graph.

There are several tools and methods available to assist in the process of graphing and analyzing linear functions. For instance, some calculators, such as Symbolab, are equipped to draw graphs, offering a visual representation to aid in understanding the equations. Furthermore, specialized solvers exist to analyze and graph linear functions, providing a more in-depth approach.

When graphing a linear function, there are several approaches one can adopt:

Plotting Points: This involves selecting at least two points and drawing a line through them. To find the points, you can use the initial value (the output when x = 0) and the rate of change (slope).
Utilizing Specific Characteristics: Another method involves focusing on the function's inherent properties rather than plotting individual points.

A system of linear equations is essentially a collection of two or more linear equations. Solving such a system means finding the point or points where the lines representing these equations intersect. The methods of solving these equations include using a graph to visually find the point of intersection. The graphs of two lines will intersect at a single point if they are not parallel. In the scenario where two lines are parallel, they will never intersect. However, two parallel lines can also intersect if they are coincident, which means they are the same line and they intersect at every point.

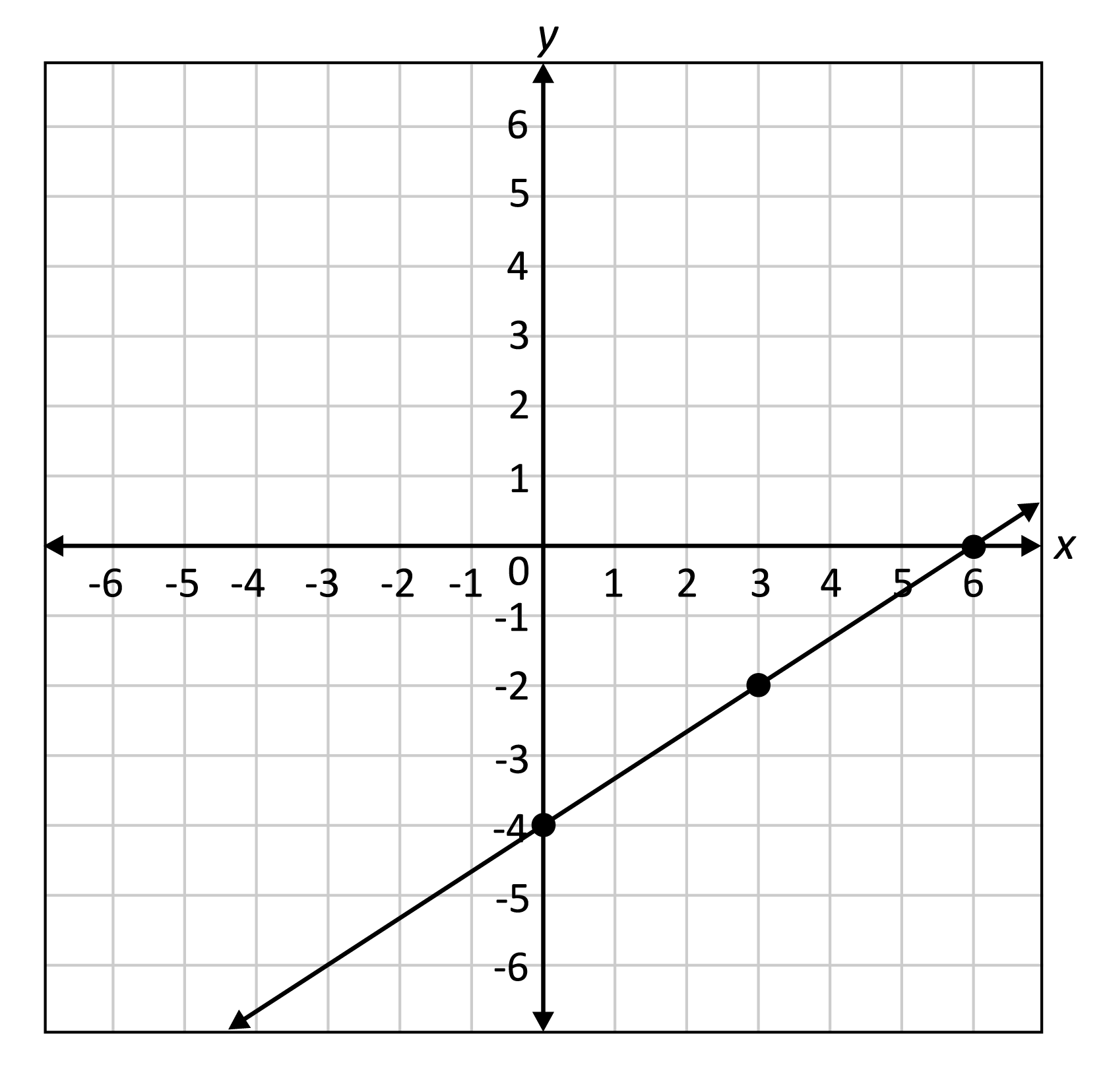
Lets delve deeper into the process. Consider a linear function. The graph of this function, as anticipated, is a straight line. This is further reinforced by the negative constant rate of change in the equation. The images above more easily visualize the relationship between the variables for each graph. You can write the equation of a linear function given its graph. You can also match linear functions with their graphs. You can find the equations of vertical and horizontal lines. Earlier, we wrote the equation for a linear function from a graph.

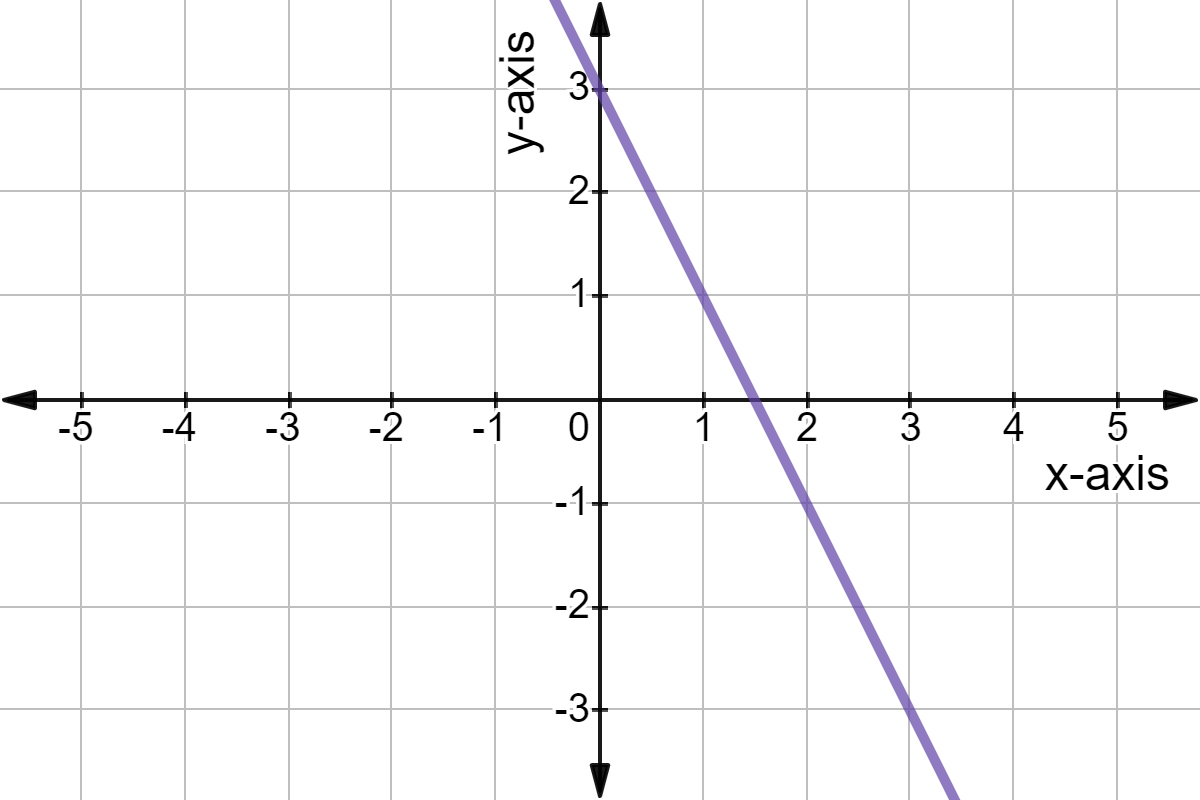
Now, we can extend our understanding of graphing linear functions to a more detailed analysis of graphs. Consider figure 18 as a starting point. In addition, the graph has a downward slant which indicates a negative slope. This is also expected from the negative constant rate of change in the equation for the function.

As an example, the equation y = 2x + 7 can be modeled by a linear function. This allows us to examine scenarios and questions, such as: Is it possible for a rectangle to have a perimeter of 5 units? Examining the graph of this linear function can explain this.

Understanding linear functions is crucial in various aspects of mathematics and real-world applications. Now we can extend what we know about graphing linear functions to analyze graphs a little more closely. Begin by taking a look at figure 8.

Here's a breakdown of the fundamental concepts and tools involved:

The Basics: A linear equation is simply an equation that describes a straight line when graphed. The graph of a linear equation is a set of points in the coordinate plane that all satisfy the equation.
Solutions: If you know an equation is linear, you can graph it by finding any two solutions (x1, y1) and (x2, y2). These solutions represent points on the line.
Visual Aids: Tools like Symbolab can draw graphs, providing a visual representation to help you understand the equations.
Methods of Graphing: There are several methods of graphing linear functions, including plotting points and using specific characteristics.

Graphing linear equations, in essence, involves transforming abstract mathematical concepts into tangible visual representations, thereby allowing us to interpret and predict the relationships between variables with greater clarity. It empowers us to see the underlying order within equations.

Let's turn to practical application: Graphing equations without a calculator Are you stuck not knowing how to draw a linear equation without using a calculator? Luckily, drawing a graph of a linear equation is pretty simple!

Here are the key takeaways:

Straight Lines are Key: A linear equation is an equation with two variables whose graph is a line.
Points and Solutions: The graph of the linear equation is a set of points in the coordinate plane that all are solutions to the equation.
Initial Value and Rate of Change: We are also able to see the points of the function as well as the initial value from a graph.

The ability to graph linear functions is not merely an academic exercise; it's a fundamental skill with real-world applications. From modeling financial data to predicting scientific phenomena, the ability to visualize and interpret linear relationships is invaluable. Whether you're a student learning the basics or a professional using data analysis, mastering this skill opens doors to a deeper understanding of the world around us.

In summary, exploring linear functions and their graphs helps us understand the characteristics more easily. In linear functions, we saw that the graph of a linear function is a straight line. The images above more easily visualize the relationship between the variables for each graph.

In conclusion, the world of linear equations, with its straightforward nature and potent visualization capabilities, provides a clear path for anyone seeking to master fundamental mathematical concepts and build a foundation for future success.

Graphing Linear Functions Examples & Practice Expii

Details

Linear Function Graphs Explained (Sample Questions)

Details

Graphing Linear Equations Examples, Graphing Linear Equations in Two

Details

Detail Author:

Name : Kali Hickle
Username : hlabadie
Email : dawn.raynor@yahoo.com
Birthdate : 1970-11-10
Address : 656 Callie Shores Suite 659 Port Aleen, DE 65938
Phone : 562.217.5247
Company : Glover-Kris
Job : Nursing Instructor
Bio : Quam corporis alias natus. Optio repudiandae ut rerum quisquam. Enim et reprehenderit quaerat accusamus tempore sed voluptatem. Commodi qui reprehenderit consectetur aut.

Socials

instagram:

url : https://instagram.com/marianobreitenberg
username : marianobreitenberg
bio : In voluptatem qui aut est ea. Nulla vel sit nobis et quia.
followers : 2570
following : 1761

twitter:

url : https://twitter.com/marianobreitenberg
username : marianobreitenberg
bio : Incidunt qui quo quod. Voluptatibus sint qui ex voluptas ratione quia. Ut quia deleniti fugit voluptates.
followers : 6461
following : 380

linkedin:

url : https://linkedin.com/in/mariano_xx
username : mariano_xx
bio : Error distinctio velit quis ipsa et.
followers : 5817
following : 586

facebook:

url : https://facebook.com/mbreitenberg
username : mbreitenberg
bio : In magnam temporibus aut. Tenetur ullam facere rerum nihil iste dolor.
followers : 667
following : 2445