Math Help: Quick Guide To Graphing & Solving Problems

22 May, 2025

Could a simple typo truly derail our pursuit of knowledge, or is there more at play when our digital queries fail to yield the expected results? The truth is, the journey through information, especially in the realm of mathematics, demands precision, yet it also offers a remarkable capacity for exploration and discovery, even when the initial path seems blocked.

We often begin with a problem, an equation, or a concept we're eager to understand. The quest starts with formulation, the initial entry. "We did not find results for:" stares back at us. A simple misspelling, a misplaced character these can indeed lead us astray. "Check spelling or type a new query." the digital assistant gently prompts. But the failure to find is not always a failure of our typing. The algorithms that power our search engines, the very tools we rely on to navigate the sea of information, can sometimes falter, misinterpreting our intentions, or simply lacking the specific data points needed to answer our question with precision. Our initial query, like the first tentative strokes of a brush on a blank canvas, is merely the beginning.

Lets consider the fundamentals. Graphing equations is a cornerstone of mathematical understanding. "Graph your problem using the following steps:" the guide suggests, providing a structured approach. "Type in your equation like y=2x+1 (if you have a second equation use a semicolon like y=2x+1 ;" it directs. The clarity of the syntax, the understanding that we can represent multiple equations on a single graph through the semicolons elegant simplicity, is a small triumph of design, making complex concepts approachable.

The power of visualization cannot be overstated. "Free graphing calculator instantly graphs your math problems." We are granted access to tools that make understanding equations almost immediately. A solid line appears, taking form and making itself clear. If we are dealing with an inequality, there is more to the process: "Graph a solid line, then shade the area above the boundary line since is" - and we can begin to work with solutions. The visual is a powerful assistant. The equation springs to life, becoming more than a string of symbols on a page, or a series of numbers. It is a picture; a thing we can see. We become the viewer, the explorer, not just the student.

The path to graphical understanding, of course, extends beyond the basic linear equation. Parabolas, those graceful curves that capture the essence of so many physical processes, become our next challenge. "Find the properties of the given parabola." The properties of the curve must be explored: the vertex, focus, directrix, and axis of symmetry. "Graph the parabola using its properties and the selected points." We can use the graph to interpret the equation. Each step is a building block, a stepping stone.

For trigonometric functions, such as sine or cosine waves, understanding takes a slightly different path. We need to work with the concepts of periodicity. "Use the form to find the variables used to find the amplitude, period, phase shift, and vertical shift." The ability to manipulate these variables offers another level of mastery. It allows us to build up waves, and by observing how each parameter affects the whole, our ability to read and understand these functions increases.

Geometry offers a wealth of fundamental concepts. "The slope of a line containing the points p 1 (x 1, y 1) and p 2 (x 2, y 2) is given by." Its a basic idea. It connects the points and gives a measure of inclination. The formula itself provides a path to understanding. "Two lines are parallel if they have the same slope (m 1 = m 2)." This simple truth unlocks a wide range of geometric problems. The connection between algebra and geometry is a profound one, a dance between numerical representation and spatial form.

Even when faced with a task, a problem that seems challenging, the path is not always straight. Sometimes, the only way forward is to break it down into smaller steps. "Tap for more stepsstep 1.1." It is a guiding principle for many problem-solving systems. Each component is easier to understand. The steps are clear. Each step forward brings us closer to a solution.

Visualizing equations and understanding mathematical concepts is only possible with the knowledge to apply the method. "Use the slope to find additional points if necessary, and label your graph and axes clearly." It's important to make the graph understandable. Clarity is key to insight, and the precision of the graph mirrors the precision of the mathematical thinking behind it.

The structure of mathematical inquiry itself is a tool. The ability to find the properties of a parabola. And, through practice, we have a path. "Graph the parabola using its properties and the selected points." Then the act itself of finding. It is repetitive, but it is also rewarding. Every success builds confidence, which then encourages us to keep going.

Mathematics is about repetition. But there is also, sometimes, a degree of serendipity in the act. "My notebook, the symbolab way." A well-stocked notebook, whether physical or digital, becomes a record of discovery. "Math notebooks have been around for hundreds of years." Their contents allow you to look back, build on past successes, and recognize patterns.

A crucial skill in all of this is the ability to manipulate equations. "Substitute for and find the result for." The substitution is a core process. It is a tool. The result is proof.

We are constantly directed to follow steps. They give order to the process. "Tap for more stepsstep 1.1." The steps are the structure. They make the goal achievable.

Mathematics is also an art. There are beautiful tools. The value is in their power. "Explore math with our beautiful, free online graphing calculator." We can draw pictures. We can make them move. "Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more." These simple tools are very powerful.

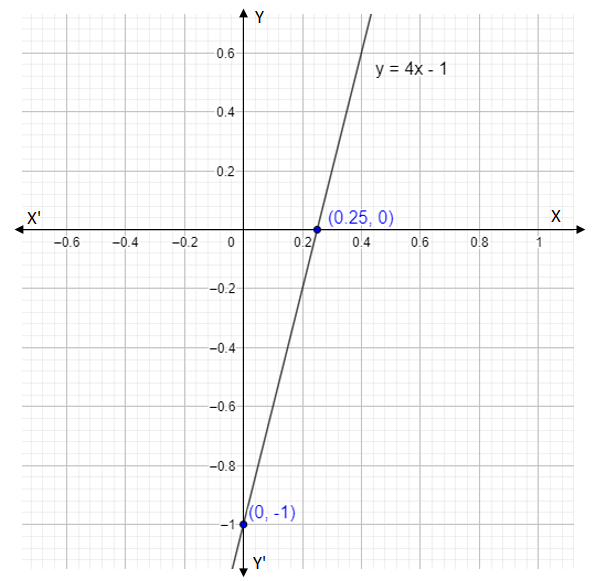
The ability to extract the meaning from numerical data is also critical. "Graph using a table of values y=4x." The table is another way to see the graph. It is a way to see the equation. The data is made real. It can be interpreted.

The process of substitution continues. "Substitute for and find the result for." This is how we practice. It is the way that we build knowledge. It is how the machine of our mind can work.

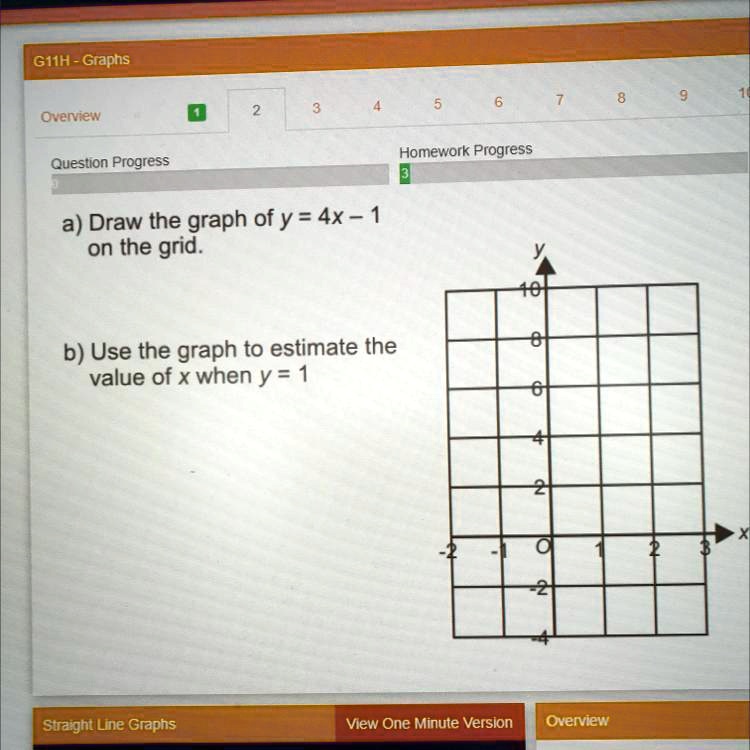
Mathematics is also practical. It is about discovering knowledge in the real world. "To find x when y = 1, draw a horizontal line from the point where y = 1 intersects the graph and that will tell us the value of x." Knowledge is power. And mathematics gives the ability to transform data into information.

Details

SOLVED 'a) Draw the graph of y = 4x 1 on the grid. In 40 8 b) Use

Details

a) Draw the graph of y= 4x 1 on the grid b) Use the graph to estimate

Details

Detail Author:

Name : Dortha Hand
Username : diego47
Email : aileen.cormier@gmail.com
Birthdate : 1971-01-27
Address : 16102 Casper Mount North Linniefurt, OR 72414
Phone : (828) 801-9837
Company : Collier-Moen
Job : Marking Machine Operator
Bio : Fugiat quo dignissimos ut ut et dignissimos. Soluta autem eum magni. Id enim repellat omnis rerum magnam a voluptatum ea. Sit quos ut quis recusandae est et omnis. Sit rerum quia soluta quis.

Socials

twitter:

url : https://twitter.com/lina_xx
username : lina_xx
bio : Magni optio sit et iste. Ut provident qui consequatur nulla aliquid autem. Beatae voluptas provident reprehenderit at aspernatur.
followers : 609
following : 2798

facebook:

url : https://facebook.com/hackett2006
username : hackett2006
bio : Id dolores sint et impedit.
followers : 6903
following : 1336

tiktok:

url : https://tiktok.com/@lina_hackett
username : lina_hackett
bio : Non vel doloribus blanditiis ratione. Officia et velit et at modi aspernatur.
followers : 3946
following : 1135

linkedin:

url : https://linkedin.com/in/lhackett
username : lhackett
bio : Aut consequatur omnis vel deserunt.
followers : 795
following : 296

instagram:

url : https://instagram.com/hackettl
username : hackettl
bio : Sunt et iure molestiae aliquid corporis et natus. Ut dolorem cumque enim inventore id.
followers : 138
following : 858