Understanding Function Graphs: A Comprehensive Guide

26 May, 2025

Ever found yourself staring at a seemingly meaningless collection of lines and curves, wondering what they truly represent? The ability to understand and interpret graphs of functions is a fundamental skill, providing a powerful lens through which we can analyze and understand the world around us.

What exactly is a function when we talk about graphing? It's not just a collection of lines on a piece of paper; it's a precise mathematical relationship. At its core, a function is a rule that takes an input, processes it, and produces a specific output. This relationship can be expressed in various ways, but the graphical representation is often the most visually intuitive. When we graph a function, we're essentially mapping the input-output pairs onto a coordinate plane. The resulting graph provides a visual story of how the function behaves, revealing patterns, trends, and critical points that might otherwise remain hidden.

To understand the essence of function, Let's imagine the survivor game where the graph representing the number of people left on an island at the end of each week, an appropriate domain would be positive integers. The black dots on the graph could tell us that the relationship between the time passed and the number of survivors left. The vertical line test is used to determine if a set in the coordinate plane is the graph of a function.

Aspect	Details
Definition of a Function	A function in graphing is a relationship between a set of inputs (the domain) and a set of possible outputs (the range), where each input is related to exactly one output.
Key Components of a Function's Graph	Domain: The set of all possible input values (x-values). Range: The set of all possible output values (y-values). Ordered Pairs: Points on the graph represented as (x, y), where x is the input and y is the output. Vertical Line Test: A test used to determine if a graph represents a function. If a vertical line intersects the graph at more than one point, it is not a function.
Representations of Functions	Equation/Formula: e.g., f(x) = x². Describes the relationship between the input (x) and output (f(x)). Graph: A visual representation of the function on a coordinate plane. Table: A table of values showing input-output pairs. Mapping Diagram: A visual representation using arrows to show the relationship between inputs and outputs.
Types of Functions and Their Graphs	Linear Functions: Graphs are straight lines (e.g., f(x) = ax + b). Quadratic Functions: Graphs are parabolas (U-shaped, e.g., f(x) = x²). Periodic Functions: (Sine, Cosine, Tangent) Graphs that repeat at regular intervals. The period is the distance from one peak to the next. Absolute Value Functions: Graphs are V-shaped. Rational Functions: Graphs often have asymptotes (vertical, horizontal, or slant). Piecewise Functions: Defined by different formulas for different intervals of the input.
Transformations of Parent Functions	Translation: Shifting the graph up/down or left/right. Reflection: Flipping the graph over an axis. Enlarging/Shrinking: Stretching or compressing the graph.
Applications	Modeling real-world phenomena (e.g., population growth, motion of objects). Analyzing data and identifying trends. Solving equations and inequalities graphically.
Tools	Graphing Calculators: Devices or online tools that can quickly plot functions. Asymptote Calculators: Tools to help determine the asymptotes of a function.
Key Terms	Period: The length of one complete cycle of a periodic function. Amplitude: The height of a periodic function from the center line to a peak (or trough). Asymptote: A line that a curve approaches but never touches.
Further Exploration	Maths is Fun - A comprehensive website for learning mathematics.

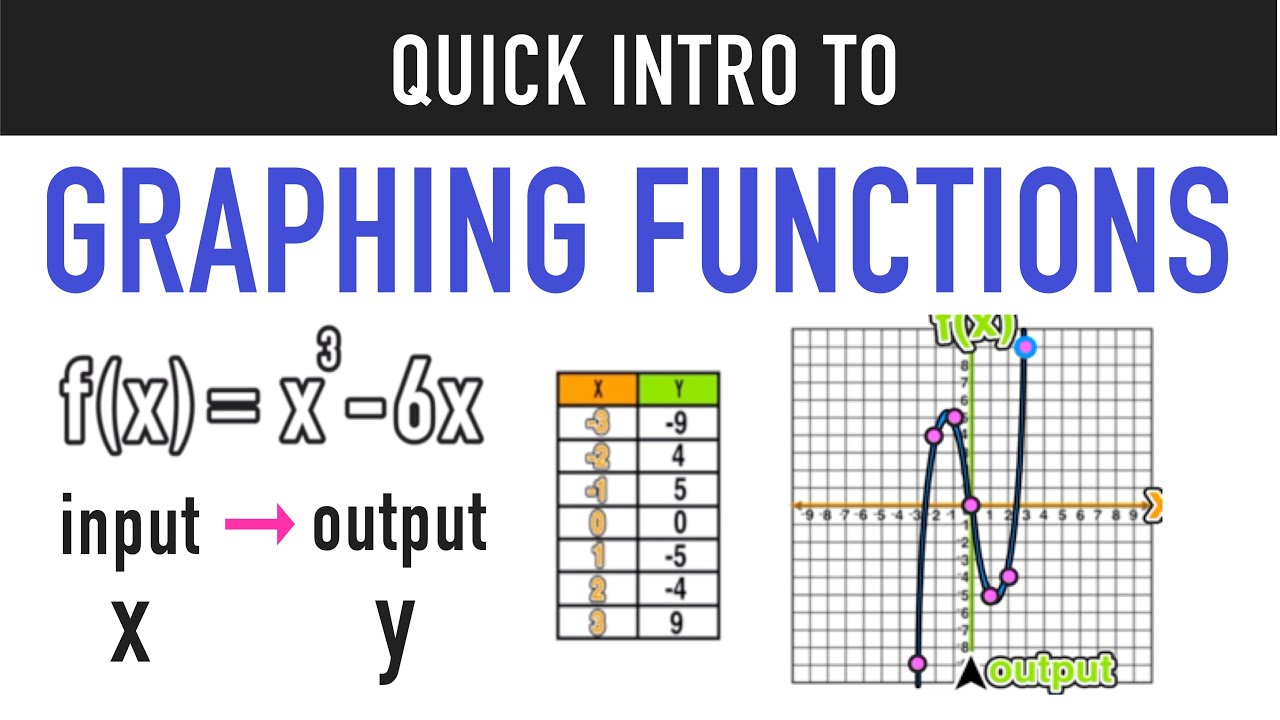
Consider a function represented by the equation f(x) = x². Here, f is the name of the function, and x is the input. The function f takes x and squares it. When we graph this, we see a parabola. The graph isn't just a random curve; it visually represents how the output changes as the input varies. We can plug different values of x into the equation to get the value of f(x), and the values can be plotted to create the graph. You could also create a table that would list a variety of x values and then the value of f(x) or y. The graph will show how the output of the function varies depending on the input.

Some functions, like sine and cosine, are known as periodic functions. These functions don't simply stop; instead, they repeat indefinitely, tracing a wave-like pattern. The period of such a function measures the length of one complete cycle. For example, the period is the distance from one peak to the next. The amplitude measures the height of the wave from its center line to its peak (or its trough). This pattern allows us to model phenomena that repeat regularly.

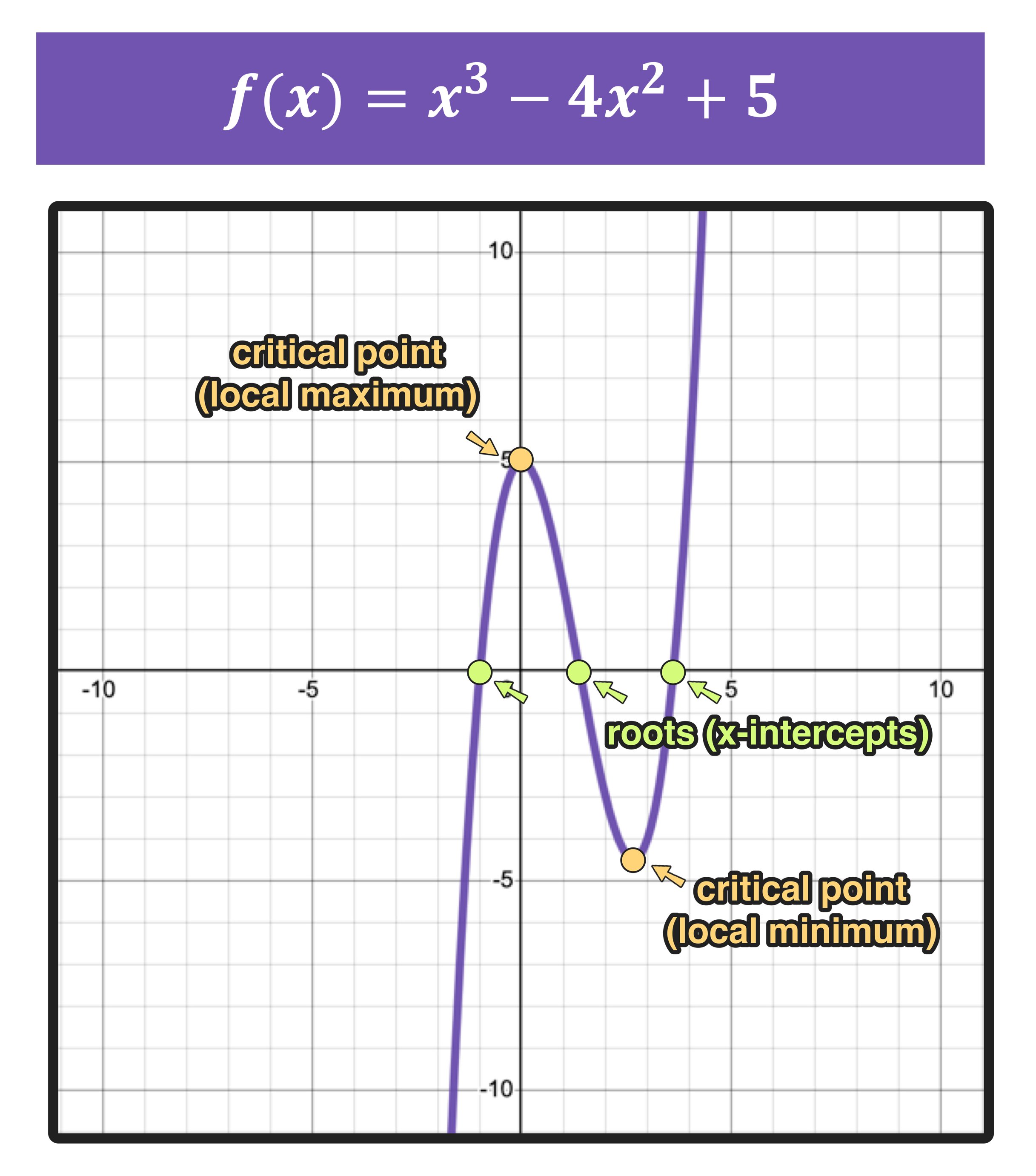
The concept of a function is a foundational concept in mathematics, and that understanding is essential for success in higher-level mathematics and many STEM fields. To determine if a graph is a function, the vertical line test is used. If any vertical line you draw intersects the graph at more than one point, it is not a function. The graph of a function is the set of all ordered pairs (x, y) where y is the output for the input value x.

Beyond the basic types of equations and formulas, variations can be created by translating, reflecting, enlarging, or applying a combination of these to its parent function graph. Graphing variations of functions allows us to observe the effects of modifying a function's equation. For example, introducing vertical and horizontal stretching or shrinking in the tangent curve.

Rational functions, which are fractions of polynomials, often have a unique characteristic: asymptotes. These are lines that the graph of the function approaches but never quite touches. Asymptotes are vital in graphing, since they provide boundaries to the function's behavior.

Piecewise functions, which are defined by different formulas across different intervals, add another layer of complexity. Graphing these requires understanding how each piece behaves and how they connect or disconnect at the interval boundaries. When graphing piecewise functions, different functions are graphed for each interval.

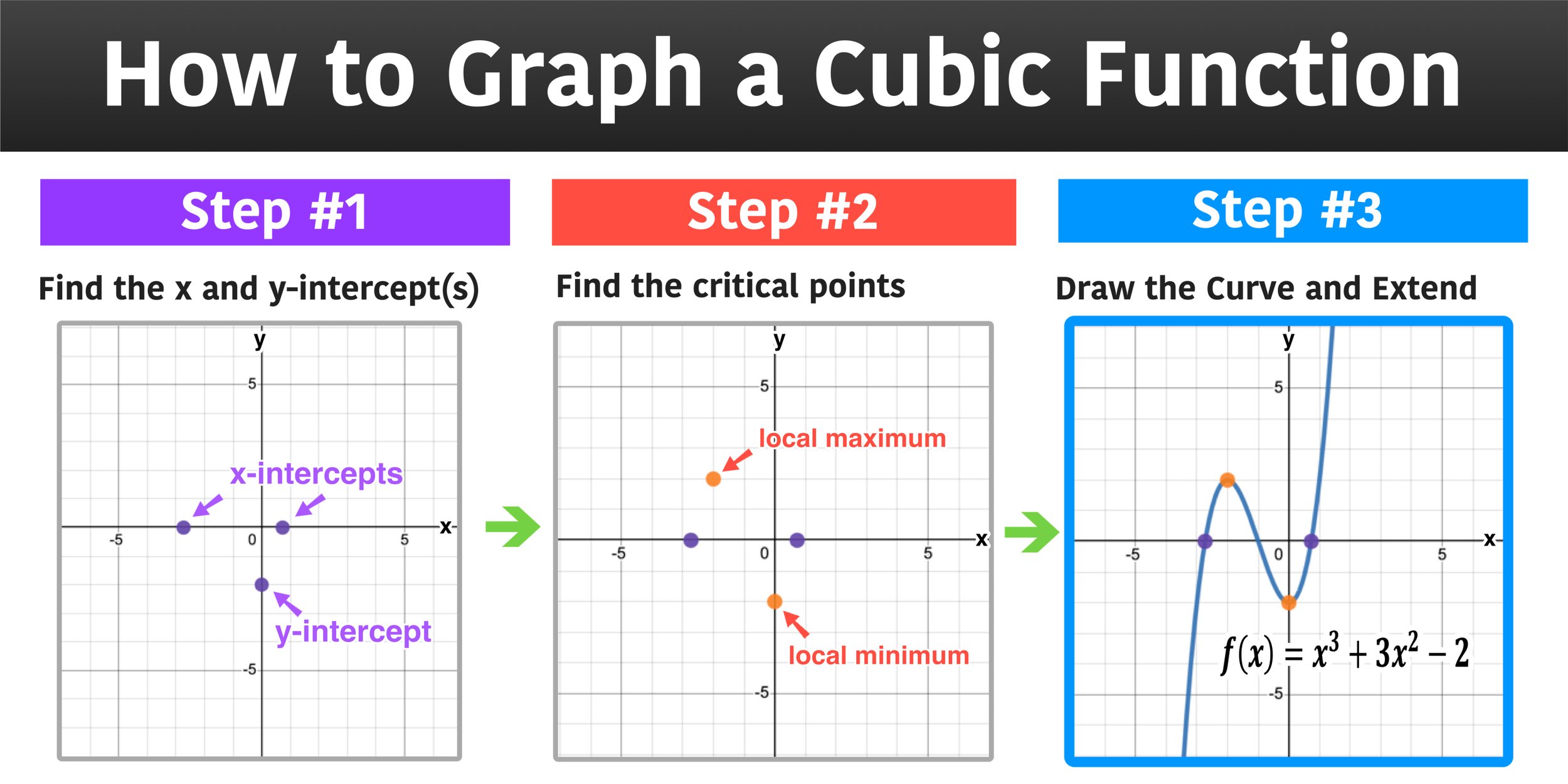
A simple approach is to calculate the function at some points. With the use of graphing calculators, you can easily enter the function you want to graph. These calculators also calculate any asymptotes, horizontal, vertical, and slant asymptotes. Then all that is needed is to click to submit to see the result.

How to Graph a Function in 3 Easy Steps — Mashup Math

Details

Details

Detail Author:

Name : Kali Hickle
Username : hlabadie
Email : dawn.raynor@yahoo.com
Birthdate : 1970-11-10
Address : 656 Callie Shores Suite 659 Port Aleen, DE 65938
Phone : 562.217.5247
Company : Glover-Kris
Job : Nursing Instructor
Bio : Quam corporis alias natus. Optio repudiandae ut rerum quisquam. Enim et reprehenderit quaerat accusamus tempore sed voluptatem. Commodi qui reprehenderit consectetur aut.

Socials

instagram:

url : https://instagram.com/marianobreitenberg
username : marianobreitenberg
bio : In voluptatem qui aut est ea. Nulla vel sit nobis et quia.
followers : 2570
following : 1761

twitter:

url : https://twitter.com/marianobreitenberg
username : marianobreitenberg
bio : Incidunt qui quo quod. Voluptatibus sint qui ex voluptas ratione quia. Ut quia deleniti fugit voluptates.
followers : 6461
following : 380

linkedin:

url : https://linkedin.com/in/mariano_xx
username : mariano_xx
bio : Error distinctio velit quis ipsa et.
followers : 5817
following : 586

facebook:

url : https://facebook.com/mbreitenberg
username : mbreitenberg
bio : In magnam temporibus aut. Tenetur ullam facere rerum nihil iste dolor.
followers : 667
following : 2445