Factoring Polynomials: Practice Problems & Resources For Algebra 2 Students
Are you ready to unlock the secrets of algebra and conquer the complexities of polynomial factoring? Mastering polynomial factoring is not just a mathematical skill; it's a gateway to understanding advanced concepts and excelling in higher-level mathematics.
The world of mathematics, often perceived as a labyrinth of abstract concepts, can be illuminated by the methodical application of certain principles. One such principle, fundamental to the understanding of algebra, is polynomial factoring. This process, seemingly complex at first glance, is in fact a systematic method of breaking down intricate mathematical expressions into simpler, manageable components. This essay aims to demystify the process of polynomial factoring, providing a comprehensive guide for both students and enthusiasts alike.
| Concept | Details |
|---|---|
| Definition | Polynomial factoring is the process of breaking down a polynomial expression into a product of simpler expressions (factors). |
| Importance | Crucial for solving polynomial equations, simplifying expressions, and understanding the behavior of polynomial functions. It forms the basis for many advanced mathematical topics. |
| Methods |
|
| Applications |
|
| Resources |
|
| Reference Link | Khan Academy - Factoring Quadratics |
The journey into polynomial factoring begins with understanding the basic building blocks: polynomials themselves. These are algebraic expressions consisting of variables, constants, and exponents, combined using addition, subtraction, and multiplication. A polynomial is characterized by non-negative integer exponents, making it a versatile tool in mathematical modeling.
- George Kittle Wife Claire Heartbreak Family Life Update
- Denzel Pauletta Washington Inside Their 40 Year Marriage
Factoring out the Greatest Common Factor (GCF) is often the initial step in simplifying a polynomial. The GCF is the largest factor that divides evenly into all terms of the polynomial. Identifying the GCF allows us to rewrite the polynomial in a more manageable form, highlighting common elements.
Consider the expression: 24x + 12x. Here, the GCF is 12x. Factoring out 12x yields 12x(2x + 1). This simple step can significantly reduce the complexity of an expression, paving the way for further factorization.
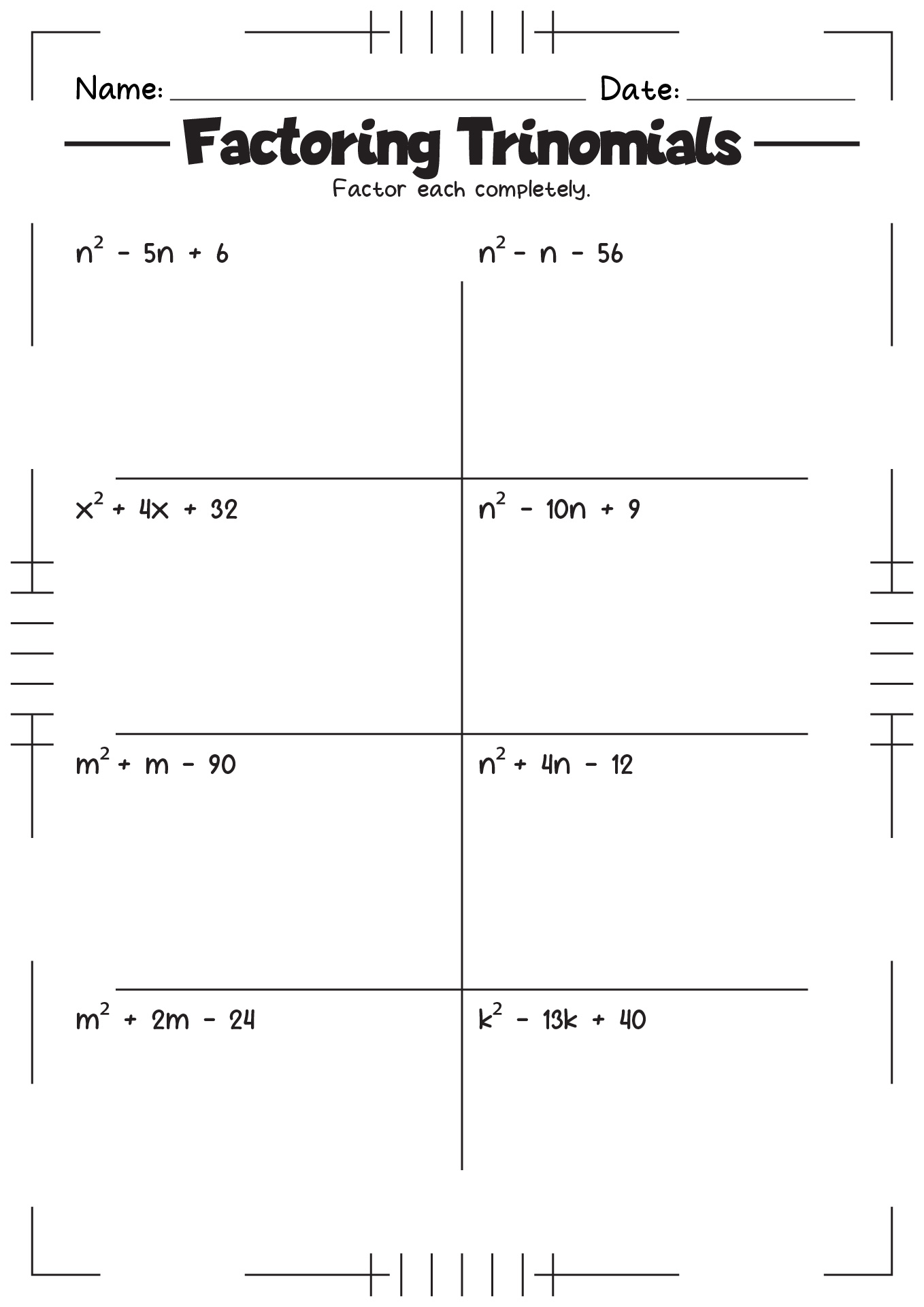
Trinomials, polynomials with three terms, present a unique challenge. They often require techniques like finding two numbers that add up to the coefficient of the middle term and multiply to the product of the first and last terms. For example, in the trinomial x + 5x + 6, we seek two numbers that add to 5 and multiply to 6. These numbers are 2 and 3, allowing us to factor the expression as (x + 2)(x + 3).
Factoring by grouping is a technique particularly useful for polynomials with four or more terms. This method involves grouping terms and factoring out the GCF from each group. Through strategic grouping, we can often reveal a common binomial factor, simplifying the expression significantly.
Special product formulas, such as the difference of squares (a - b = (a + b)(a - b)) and the sum/difference of cubes (a b = (a b)(a ab + b)), provide shortcuts for factoring specific forms of polynomials. Recognizing these patterns can save time and effort, transforming complex expressions into easily manageable factors.
In practice, factoring polynomials involves a combination of these techniques. The goal is to break down the expression into its irreducible factors, which can then be used for solving equations, simplifying expressions, and analyzing the behavior of polynomial functions.
The application of polynomial factoring extends far beyond the classroom. It is essential for various fields, including engineering, physics, and computer science. In engineering, factoring is used to analyze circuit behavior, design structures, and optimize system performance. In physics, factoring is crucial for solving equations of motion, analyzing projectile trajectories, and understanding wave phenomena. Computer scientists utilize factoring in algorithms for data compression, cryptography, and software development.
Mastering polynomial factoring is an investment in the future. As students progress through their mathematical education, they will encounter more complex applications of factoring, from calculus to differential equations. By developing a solid understanding of the basics, students equip themselves with a powerful tool for tackling advanced concepts.
The notes for Paul Dawkins' Algebra course at Lamar University provide excellent practice problems to hone factoring skills. Resources like Mathbitsnotebook offer free lessons and practice exercises. For those seeking additional support, websites like Khan Academy provide comprehensive instruction and interactive exercises. Calculators such as Cymath and Symbolab can assist in checking answers and gaining further insight into the solution process.
The provided content includes examples of factoring problems, such as:
- Factoring out a GCF, then trinomial:
- (a) t - 11t + 28
- (b) 7m + 25m + 12
- (c) 24x + 44x + 40
The solutions typically involve finding the factors of the constant term that satisfy the conditions of the problem. For instance, in the first example, the factor pairs of 28 are considered in relation to the coefficient of the middle term (-11) to find the correct factors.
Additional practice problems, like those listed below, offer an opportunity to apply different factoring techniques:
- R + 3r + 2
- 10n - 35 = 65n
- 3x - 8x = 16
- 16n - 114n = -14
- 28n = -96 - 184n
- 7a + 32 = 7 - 40a
- 42x - 69x + 20 = 7x - 8
The various solving methods that can be learned include:
- Factoring a sum/difference of cubes
- Factoring by grouping
- Factoring quadratic form
- Factoring using all techniques
- Factors and zeros
- The remainder theorem
- Irrational and imaginary root theorems
- Descartes' rule of signs
- The rational root theorem
The use of algebra 2 polynomial worksheets is encouraged, as they generate problems utilizing all techniques, allowing for the selection of the degree of the polynomials. These resources are beneficial to building comfort with the concept.
Factoring is also employed when solving polynomial equations. This technique is particularly useful for solving quadratic and higher-degree equations. Factoring enables the isolation of individual factors and setting them equal to zero, to identify the roots or solutions to the equation. This process is integral for determining where a polynomial function crosses the x-axis.
Furthermore, factoring by grouping is a method that can be used in relation to quadratic expressions (ax + bx + c). When presented with a four-term polynomial, it involves grouping pairs of terms, factoring out the GCF from each group, and then factoring out the common binomial. This technique proves invaluable in simplifying expressions that do not immediately fit other factorization patterns.
For those looking to deepen their understanding, exploration of the relationships between factoring and other algebraic concepts, such as the Remainder Theorem, the Factor Theorem, and the Rational Root Theorem, is advisable. These theorems provide additional tools for verifying factors, finding zeros, and determining the behavior of polynomials.
The importance of practice cannot be overstated. By working through a variety of problems, students reinforce their understanding of the different factoring techniques, build confidence, and develop the problem-solving skills necessary for success in higher-level mathematics.
In conclusion, polynomial factoring is an essential skill in algebra and beyond. By understanding the fundamental concepts, mastering the various techniques, and practicing regularly, students can unlock the power of polynomials and pave the way for success in advanced mathematical studies and related fields. The resources available, from online platforms to practice problems, are ample, enabling students to explore the world of polynomials with confidence and precision. The journey of mastering polynomial factoring is a rewarding one, providing a solid foundation for future mathematical endeavors.

Detail Author:
- Name : Fannie Sawayn
- Username : carmine.mcclure
- Email : leffler.payton@yahoo.com
- Birthdate : 2004-08-22
- Address : 2108 Bergstrom Rue Port Pierce, HI 84141-7618
- Phone : +1-863-969-0109
- Company : Shanahan, Schiller and Reilly
- Job : Farmworker
- Bio : Aut possimus ea temporibus dolorum voluptatem vero voluptatum. Asperiores in aut necessitatibus perferendis et numquam. Culpa in qui reprehenderit et voluptas beatae omnis rerum.
Socials
instagram:
- url : https://instagram.com/einarconn
- username : einarconn
- bio : Laudantium eos quia consectetur architecto. Earum ut rem illo non recusandae qui non.
- followers : 5656
- following : 2115
twitter:
- url : https://twitter.com/conne
- username : conne
- bio : Id adipisci expedita aut velit. Maiores aliquam et eligendi vitae quam illum ea.
- followers : 391
- following : 717
tiktok:
- url : https://tiktok.com/@econn
- username : econn
- bio : Est aut voluptas aut expedita magnam et sunt.
- followers : 393
- following : 1160