Graph Domain & Range: A Complete Guide!

26 May, 2025

Are you ready to unlock the secrets hidden within the curves and lines of mathematical graphs? Understanding the domain and range is fundamental to truly grasping the behavior of functions and the stories they tell.

We often find ourselves at the intersection of art and science when we approach the world of mathematics. Graphs, in particular, offer a visual feast, transforming abstract equations into tangible forms. But to truly appreciate these visual narratives, we must first understand the language in which they are written: domain and range.

Let's start with some foundational definitions. In the context of a function, the domain can be thought of as the set of all possible input valuesthe values you can "feed" into the function. Think of it as the x-axis, the horizontal pathway along which the function operates. The range, on the other hand, is the set of all possible output valuesthe values the function produces. This is the y-axis, the vertical dimension that reflects the function's response to the inputs.

The range of a function can be determined using different types of data representation. This includes ungrouped data, frequency distribution tables, and graphical tools such as histograms, boxplots, and scatterplots. However, calculating the range from raw data, is a fundamental skill. It's the difference between the maximum and minimum values within a dataset. This simple calculation unveils the span of the data, providing immediate insights into its spread.

When working with graphs, especially with the help of interactive tools, like online graphing calculators, you often have the ability to customize the viewing window. Parameters like "x min," "x max," "y min," and "y max" allow you to zoom in on specific sections of the graph, enhancing the precision and focus of your analysis. You can also change the grid size and resolution, refining the level of detail. Checkboxes allow you to display or hide essential elements like axes and labels, and the plotting of your functions is just a click away. The best online graphing tools bring equations to life, plotting points, animating graphs, and giving you a visual grasp of algebraic equations, sliders, and more.

Let's consider a practical example to further illuminate these concepts. Imagine we're analyzing a function, f(x), that represents the growth of a population over time. The domain would be the possible time values (e.g., years, months), and the range would be the corresponding population sizes. Pictures greatly ease the process of visualizing the domain and range of functions. They assist us with easily understanding how they behave when viewed through graphical representations.

Now, consider a linear function, a straight line that extends infinitely in both directions. The domain of such a function typically encompasses all real numbers, as there are no restrictions on the input values. The range is also typically all real numbers, as the function's output can take on any value. However, the domain and range can shift depending on the specific context of the problem.

In contrast to linear functions, trigonometric functions present a different set of challenges. The graphs of the six primary trigonometric functions (sine, cosine, tangent, cotangent, secant, and cosecant) exhibit periodic behavior and have specific domains and ranges that are critical to comprehend. The values of input where the function is not defined must be thoroughly checked and considered.

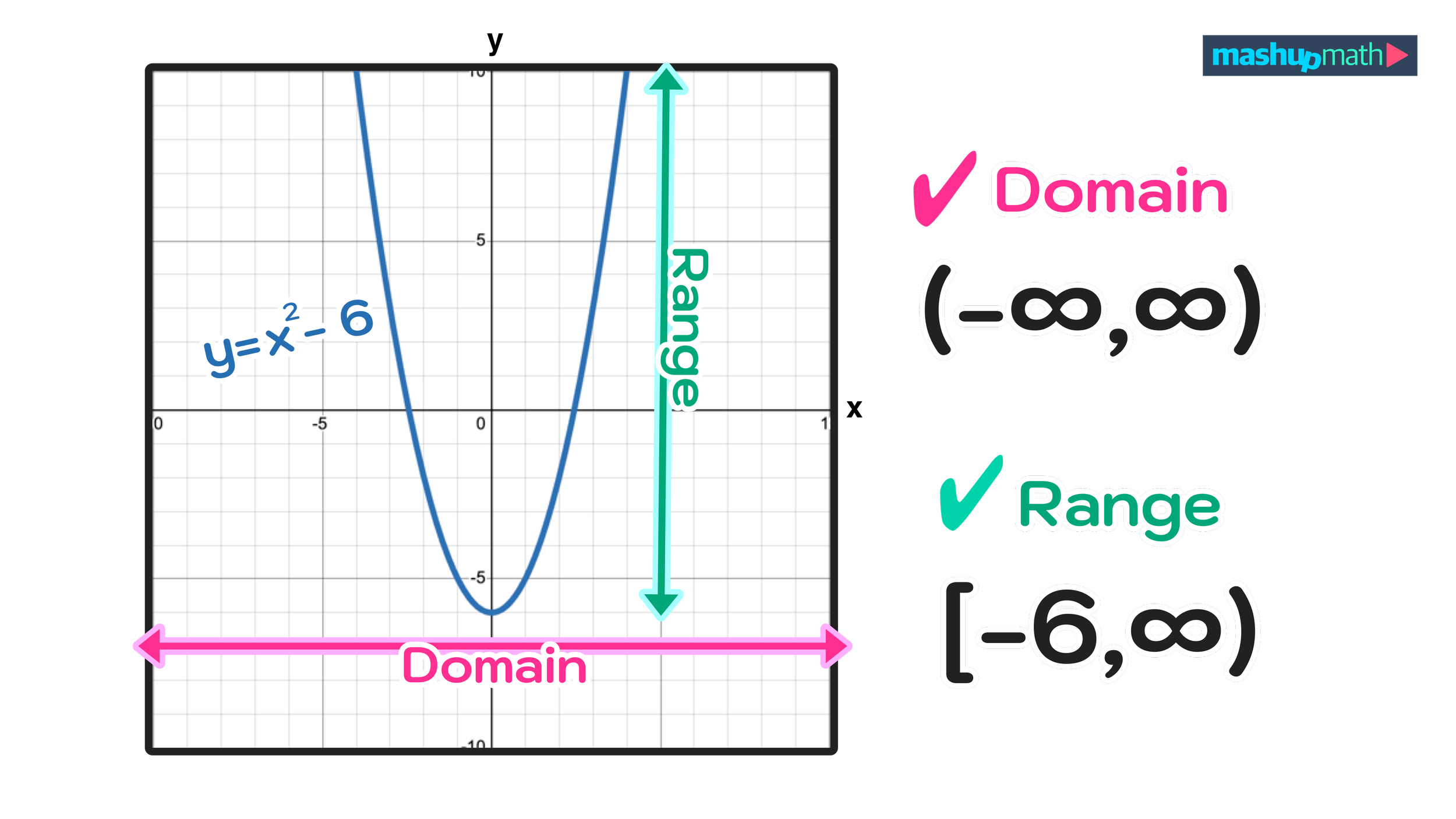
Graphs provide an accessible means to ascertain the domain and range of a function. The domain is composed of the input values displayed on the graph, and the range comprises the output values. Input values are nearly always displayed along the horizontal axis of a graph, giving context to the domain.

Creating graphs is also extremely helpful in understanding and interpreting data. Creating graphs in applications such as Google Sheets transforms numbers into visual insights that are easier to grasp. The art of selecting the right data range for your graph is crucial to ensure your graphs accurately represent the information. Such actions are a crucial step in ensuring that your graphs accurately represent the information you want

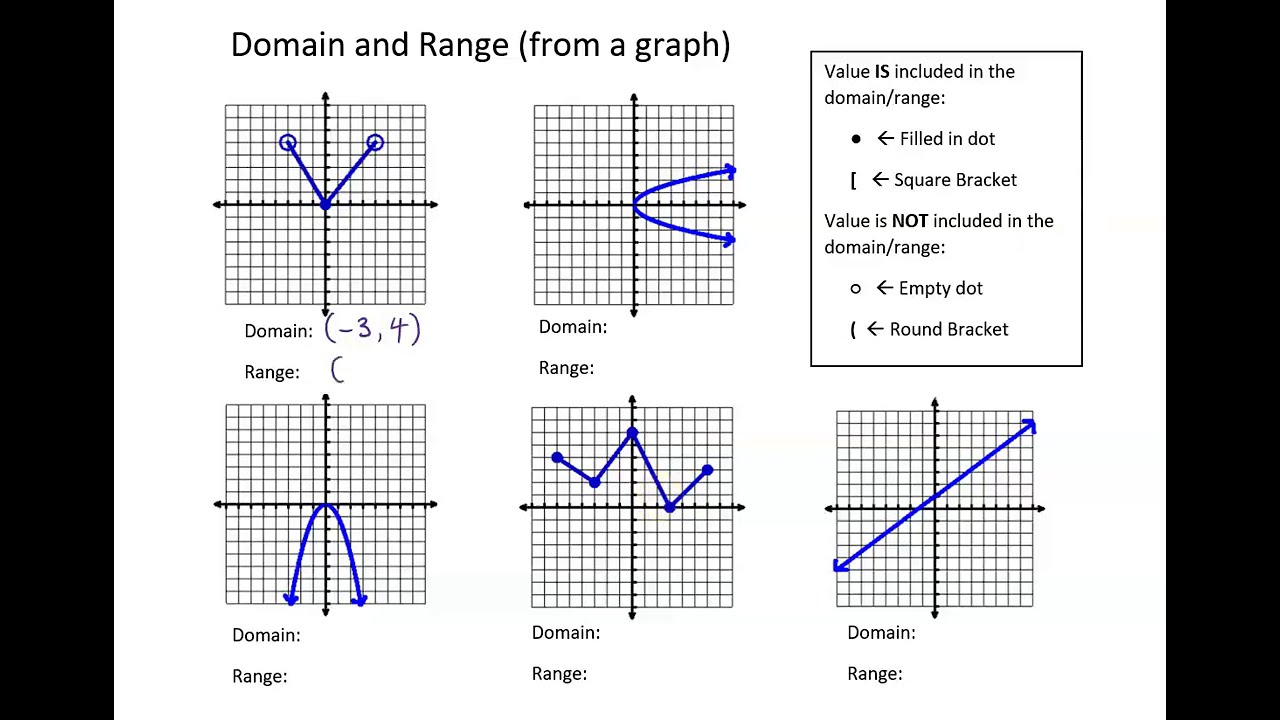
The steps to find the range from a graph involve identifying the minimum and maximum y-values. These values define the boundaries of the range. It's also necessary to consider the behavior of the function at the endpoints of its domain. Closed circles (filled-in dots) indicate that the endpoint is included in the range, while open circles (empty dots) indicate that the endpoint is not included.

Consider a scenario where a graph demonstrates a relationship between time (t) and a variable (b). Based on the graph's visible portion, we determine the domain as [1973 t 2008] and the range as roughly [180 b 2010]. In interval notation, the domain becomes [1973, 2008], and the range is approximately [180, 2010].

Furthermore, it is vital to recognize that the range can include both negative and positive numbers. We do not incorporate it into the range, as a graph contains an open circle. Therefore, in interval notation, the domain becomes [1973, 2008], and the range is roughly [180, 2010].

Being able to identify the domain and range of a graph function and expressing the domain and range using interval notation are essential algebra skills. However, if the graph proceeds further, the domain and range may be greater than what the current values show. If it has both a minimum and maximum, the range could be [a, b].

As such, the interval of values is the set. When looking at a graph, the domain is all the values of the graph from left to right. The range is all the values of the graph from down to up. The domain refers to the set of possible input values, and the range is the set of possible output values.

The set of x values covered by the graph is the domain, and the set of y values covered by the graph is the range. However, we must also consider these elements while writing the domain and range of a graph. We must check whether the graph passes the vertical line test.

In essence, the domain and range are the twin pillars upon which our understanding of functions rests. By mastering these concepts, we equip ourselves with the tools to decipher the language of graphs, revealing the hidden patterns and relationships that shape our world. So, the next time you encounter a graph, remember that you are not just seeing lines and curvesyou are reading a story, and domain and range are the keys that unlock its meaning.

How to Find Domain and Range of a Graph (Step by Step) — Mashup Math

Details

Details

Detail Author:

Name : Halie Quitzon
Username : hegmann.jerrold
Email : rylan57@tremblay.com
Birthdate : 1983-03-06
Address : 6414 Linwood Cliffs Lake Teaganville, DE 77784
Phone : 303-573-7154
Company : Bradtke Ltd
Job : Fabric Pressers
Bio : Et cupiditate voluptas vel quaerat aut est nam et. Et quia reprehenderit quasi est eos nemo. Quo rem ea sapiente ad molestiae esse dolor.