Function Grapher: Your FREE Online Tool! Plot & Explore

22 May, 2025

Can a single image truly unlock the secrets of a complex mathematical function? Yes, the power to visualize equations, dissect their behavior, and understand their essence is readily available through the simple act of graphing. This seemingly straightforward process is a cornerstone of mathematical exploration, offering a window into the hidden relationships between variables and the dynamic world they inhabit.

Graphing functions is more than just drawing lines on a grid; it's a visual language that speaks volumes about the underlying mathematical principles. Whether you're a student grappling with algebra, a scientist exploring the intricacies of data, or simply a curious mind seeking to understand the world around you, the ability to graph functions is an invaluable skill. This article delves into the world of graphing, providing a comprehensive guide to understanding and utilizing these powerful tools.

The journey begins with understanding the fundamental concepts. A function, in its essence, is a relationship between two sets of numbers: the inputs (the domain) and the outputs (the codomain). The function takes an element from the domain and transforms it into a corresponding element in the codomain. This relationship can be represented in various ways, but the most visually compelling is the graph. Graphing, in essence, is the process of plotting the curve of the function, providing a visual representation of how the output changes in response to the input.

The process itself involves plotting points on a Cartesian coordinate system (a grid defined by two perpendicular axes, typically labeled x and y). For each input value (x), the function calculates an output value (y), and this pair of numbers (x, y) represents a point on the graph. By plotting a sufficient number of points and connecting them, we can visualize the function's behavior. Understanding how to graph functions is a building block, whether you're charting the course of a rocket, analyzing stock market trends, or simply satisfying your curiosity.

Heres a look at the core concepts and mechanics that underpin graphing functions. Lets start with the basics. You can leverage the power of function graphers. These digital tools are specifically designed to render complex equations and allow you to explore their properties. By using these interactive calculators, you can visualize algebraic equations, add sliders to adjust parameters, and even animate graphs to gain deeper insights. The beauty of these tools lies in their ability to remove the computational burden, allowing you to focus on the interpretation and understanding of the functions themselves.

Consider the equation \(y = x^2 + 1\). This is a quadratic function, and its graph is a parabola. To graph this function, you would first select several values for x (the input). For each x-value, you would calculate the corresponding y-value (the output) using the equation. For instance:

If x = -2, then y = (-2)^2 + 1 = 5. This gives us the point (-2, 5).
If x = -1, then y = (-1)^2 + 1 = 2. This gives us the point (-1, 2).
If x = 0, then y = (0)^2 + 1 = 1. This gives us the point (0, 1).
If x = 1, then y = (1)^2 + 1 = 2. This gives us the point (1, 2).
If x = 2, then y = (2)^2 + 1 = 5. This gives us the point (2, 5).

Now, you would plot these points on a coordinate plane and connect them with a smooth curve. This curve represents the graph of the function \(y = x^2 + 1\).

The functionality of a function grapher extends far beyond just plotting a single equation. Many graphers allow you to compare multiple functions simultaneously. For instance, you could graph \(y = x^2 + 1\) alongside \(y = 2x - 1\) to find the points of intersection. These intersection points are crucial; they represent the x-values where the two functions produce the same output. You can select curves of interest to see points of interest.

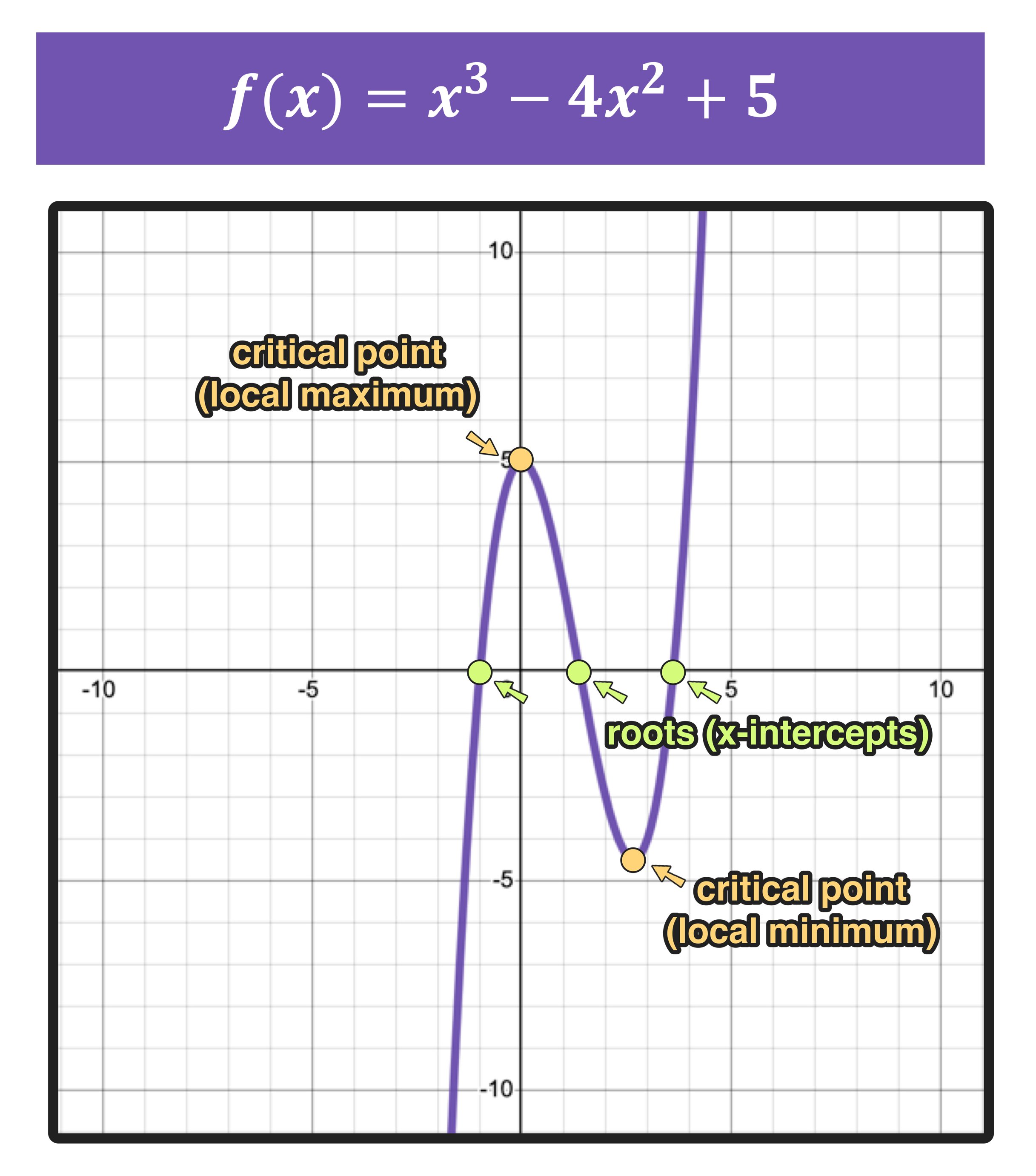
Graphing extends to a variety of function types, each exhibiting unique characteristics. Linear functions, defined by the equation \(y = mx + b\), produce straight lines, where 'm' represents the slope (how steeply the line rises or falls) and 'b' represents the y-intercept (where the line crosses the y-axis). Quadratic functions, like our example \(y = x^2 + 1\), generate parabolas, characterized by their U-shaped or inverted U-shaped curves. Cubic functions, involving x-cubed terms, produce curves with more complex shapes, often with points of inflection. Even more complex functions, like rational functions (fractions involving variables) and logarithmic and exponential functions, are within the grasp of the grapher. The key is to select the correct tool for the job. A function grapher is designed to work with explicit functions, while an equation grapher is more versatile but may sometimes be a little slower or give inaccurate results.

The power of graphing also extends to more complex mathematical explorations. For example, you can use a graphing calculator to find the equation of a linear function, given two points on its graph. This involves calculating the slope of the line and then using the point-slope form of a linear equation. These tools are useful whether you're learning about mathematical functions or analyzing scientific data, plotting and graphing make it easier to understand and work with functions.

Online graphing calculators have become a valuable resource. Their capabilities include the ability to visualize algebraic equations, plot data, manipulate sliders to observe parameter changes, and even create and analyze complex geometric shapes, like triangles and circles. The best online graphing calculators are those that offer interactivity, allowing users to dynamically explore functions and equations. Wolfram|Alpha is also one of those useful tools. These tools are reliable sources for computation across different subjects.

The availability of these interactive tools makes exploring math accessible to a wider audience. They empower students, educators, and professionals to understand and visualize mathematical concepts. Functions can take elements from a set (the domain) and relate them to elements in a set (the codomain).

One of the main strengths is that it also gives the option of saving your work and using it at any time by its url(website link).

To get started, simply type the function into the input box. Use 'x' as the variable. After you type your equation, the graph appears instantly. Adjust the graph by zooming or panning to explore different parts of the function. A good graphing calculator should have multiple functions, so that the user can add a number of functions to analyze and see their similarities or points of intersection. You can customize the graphs and save them as svg files. With these tools, you can gain additional perspective by studying polar plots, parametric plots, contour plots, region plots and many other types of visualizations.

You can customize the appearance of the graphs, adjust the axes, and add labels to make your visualizations clearer and more informative. The grapher application is split into tabs. In the expressions tab, you can choose from a variety of templates or start from scratch. The grapher supports functions, conics and inequalities as well as parametric and polar curves.

Not all graphs represent functions. Consider the Vertical Line Test, which is the method of determining if a graph represents a function. If any vertical line intersects the graph at more than one point, the graph does not represent a function. The examples above were graphs of functions, but in the last section we talked about graphing relations and not just functions. To determine whether something is a function, make sure that for every input, there is only one output.

However, functions are going to be the focus of what we work with in this course so this brings us to an important question: How do we know if a graph represents a function?

Plotting and graphing are methods of visualizing the behavior of mathematical functions. Whether you're plotting functions, visualizing algebraic equations, adding sliders, or animating graphs, the goal remains the same: to transform abstract mathematical concepts into tangible, understandable visual representations. These are crucial tools to enhance one's understanding of mathematical concepts.

In contrast, an equation grapher is more versatile than a function grapher. It can handle various types of functions and curves, such as explicit, implicit, polar, and parametric.

Now, let's delve into the practical application of graphing. Suppose you want to visualize a rational function, such as \(f(x) = \frac{1}{x}\). This function has a unique behavior: it's undefined at x = 0 and has horizontal and vertical asymptotes. To graph this, you would follow these steps:

Create a table of x and y values, avoiding x = 0. For example:
- x = -2, y = -0.5
- x = -1, y = -1
- x = 1, y = 1
- x = 2, y = 0.5
Plot the points on the coordinate plane.
Notice that the graph approaches, but never touches, the x-axis and the y-axis. These are the asymptotes.
Draw two separate curves, one to the left of the y-axis and one to the right, approaching the asymptotes.

Graphing the rational functions requires understanding of asymptotes. This simple function example illustrates how graphing helps in analyzing the behavior of equations.

In summary, graphing functions is an invaluable tool in mathematics and beyond. It's a visual language that allows you to explore the relationships between variables, understand complex concepts, and gain insights into the world around you. By mastering the techniques and utilizing the available tools, you can unlock the power of graphing and embark on a journey of mathematical discovery.

The journey doesn't end with knowing how to graph; it extends to understanding the nuances of different function types, their properties, and their applications in various fields. From the straight lines of linear functions to the curves of quadratic and exponential functions, each type reveals a unique aspect of mathematical modeling.

Interactive graphing tools also allows for the creation of a wide array of visualizations. By using these interactive graphing tools, you're not merely plotting data; you're dynamically exploring relationships and gaining a deeper understanding of mathematical principles. These resources offer an ideal blend of functionality and accessibility.

How to Graph a Rational Function 8 Steps (with Pictures)

Details

How to Graph a Function in 3 Easy Steps — Mashup Math

Details

Details

Detail Author:

Name : Glenna Rohan DVM
Username : alfreda80
Email : joshuah50@hotmail.com
Birthdate : 1994-07-20
Address : 315 Domenic Fort Apt. 929 Yessenialand, KS 91830-7816
Phone : 1-283-873-4138
Company : Hayes and Sons
Job : Compacting Machine Operator
Bio : Fugiat earum omnis voluptatibus rerum velit. Eaque tempore qui velit maxime. Aut voluptatem dolores dolor vel facere.

Socials

instagram:

url : https://instagram.com/blaze_kiehn
username : blaze_kiehn
bio : Sint qui labore reiciendis quisquam. Necessitatibus at ab quos reprehenderit.
followers : 6557
following : 231

tiktok:

url : https://tiktok.com/@blaze_kiehn
username : blaze_kiehn
bio : Dolor aut sequi et illum deserunt.
followers : 6629
following : 353

facebook:

url : https://facebook.com/kiehnb
username : kiehnb
bio : Corporis delectus cupiditate perspiciatis quod nulla.
followers : 1868
following : 879

linkedin:

url : https://linkedin.com/in/kiehn2012
username : kiehn2012
bio : Adipisci architecto modi dolorum sed et nostrum.
followers : 2988
following : 2402

twitter:

url : https://twitter.com/blaze.kiehn
username : blaze.kiehn
bio : Rerum omnis sunt qui. Voluptatem et suscipit consequatur culpa. Iure in ullam nam odit illum.
followers : 3888
following : 442