Graphing & Equations: 8th Grade & High School Math

25 May, 2025

Can a free graphing calculator truly revolutionize the way we approach math problems? Yes, the instant accessibility of graphing calculators, particularly web-based ones, fundamentally changes how students learn and solve math, from basic algebra to advanced calculus.

The digital age has brought forth a plethora of tools designed to simplify complex tasks, and mathematics is no exception. Free graphing calculators, readily available online, are changing the landscape of math education and problem-solving. Platforms such as Mathway offer instant graphing capabilities, allowing users to visualize equations and functions with ease. But how exactly do these tools fit into the curriculum of 8th-grade math and high school math? Their impact is multifaceted, providing both immediate assistance and a deeper understanding of mathematical concepts.

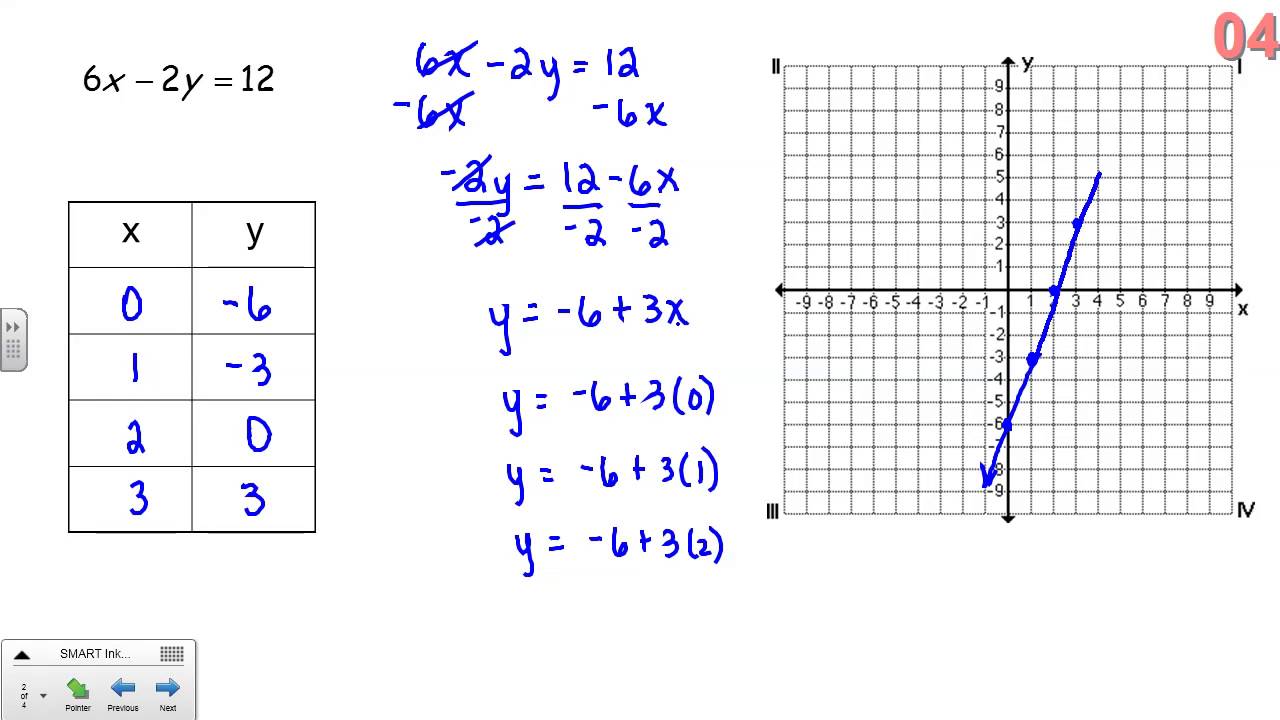
In the realm of 8th-grade mathematics, students are introduced to fundamental concepts such as linear equations, graphing, and basic functions. A graphing calculator allows students to visually explore these concepts, reinforcing their understanding of slopes, intercepts, and the relationship between equations and their graphical representations. Consider the equation y = 2x + 1. Traditionally, students would need to plot points manually to graph this equation. Now, with a graphing calculator, they can instantly visualize the line, experiment with different values, and gain a concrete understanding of how the slope and y-intercept affect the line's position.

High school math, on the other hand, delves into more complex topics like quadratic equations, trigonometric functions, exponential functions, and calculus. Graphing calculators become indispensable tools in these areas. They facilitate the exploration of complex graphs, the identification of key features such as vertices, asymptotes, and intercepts, and the solution of equations that would be otherwise cumbersome to solve manually. For instance, when dealing with a parabola represented by the equation y = x 4x + 3, students can quickly graph it to find its vertex, axis of symmetry, and x-intercepts. Similarly, when working with trigonometric functions, calculators enable students to visualize sine and cosine waves, understand their properties, and solve related equations.

The core of understanding mathematical concepts lies in the ability to represent and manipulate equations and functions visually. The advent of free graphing calculators allows students to do precisely that. The equation y = mx, representing a line through the origin, can be quickly visualized, and the impact of the slope (m) on the line's steepness and direction becomes immediately apparent. Similarly, the equation y = mx + b, where 'b' is the y-intercept, allows students to understand how a line shifts vertically. The ability to see these equations in action fosters a deeper understanding of their underlying principles.

Beyond the basic application of graphing, these tools also provide opportunities for exploring more complex mathematical models. Consider an exponential function. Given its graph, finding the equation becomes a matter of identifying the initial value and the constant ratio, both of which can be easily visualized and calculated using the graphing calculator's features. For example, an equation might be represented as f(x) = 2.4492(0.6389)^x. The graphing calculator facilitates the verification of this equation by allowing students to plot the model and compare it to the original graph. This process of visual confirmation strengthens the understanding of exponential growth and decay.

The value of a graphing calculator extends beyond mere computation and visualization. It serves as a powerful tool for problem-solving. Consider the task of finding the equation of a line given two points. The steps involve calculating the slope, and then using the point-slope form or slope-intercept form to derive the equation. The calculator simplifies this process by allowing students to input the points, calculate the slope, and graph the line, providing an immediate visual confirmation of their solution. It is worth noting that the ability to graph a quadratic equation enhances the understanding of its properties, from its vertex to its intercepts, while simultaneously supporting the practice of problem-solving skills.

Trigonometry is another area where graphing calculators prove invaluable. When finding the equation of a sine or cosine wave, students need to identify the amplitude, period, and phase shift. The calculator simplifies this process by allowing students to graph the function and identify these key features visually. The amplitude, which is half the distance between the maximum and minimum points of the wave, can be easily measured from the graph. Similarly, the period and phase shift can be deduced from the graph, allowing students to construct the equation of the trigonometric function accurately.

The use of graphing calculators also extends to more advanced topics such as data analysis and statistics. The tools allow students to graph scatter plots, create linear trendlines, and analyze data sets. By choosing the "linear" option in the graphing tool and checking the "display equation on chart" feature, students can find the equation of the trendline, allowing them to model and predict trends in real-world data.

Polynomial functions, especially cubic functions and higher-order polynomials, can be explored and graphed using these calculators. Selecting the polynomial option and setting the desired order allows students to visualize the behavior of these functions, understand their roots, and analyze their properties.

The capacity to represent and resolve equations, and their corresponding graphs, is a fundamental skill in mathematics. A linear equation, defined by a straight line, is clearly represented on a graph. One can utilize multiple techniques to graph a linear equation, and, in this example, y = 2x + 1 can be easily graphed by plotting points. To create this, one can begin with the basic algebraic equations, and use their values to extend the line from the y intercept, b. This practice offers students direct visual confirmation for their algebraic equations.

The exploration of geometric shapes is another application of graphing calculators. For instance, the ability to put a circle of radius 5 on a graph allows students to visualize and understand the relationship between the equation x + y = 5 and the circle's properties. Finding points on the circle becomes an exercise in applying the equation and understanding its geometric implications.

In essence, free graphing calculators empower students to engage with mathematics in a more dynamic and interactive way. They transition from passive recipients of information to active explorers of mathematical concepts. This shift not only makes learning more engaging but also fosters a deeper, more intuitive understanding of the subject matter. The availability of these tools democratizes access to powerful mathematical capabilities, making complex concepts accessible to a wider range of students. Furthermore, they support the development of problem-solving skills, as students can quickly test hypotheses, experiment with different values, and visualize the impact of their choices.

Identifying features of a parabola from its equations or graphs allows students to grasp a wider range of mathematical functions. From this, one can further identify the orientation, vertex, axis of symmetry, min/max points, domain and range, and intercepts of any function. Similarly, students can gain understanding by converting between general and vertex forms by utilizing the features in the calculator.

When encountering a graph and the corresponding exponential equation needs to be determined, the key features to identify are the initial value and the constant ratio. These steps make the complex process easier for the students to understand. They create a strong foundation for the mathematical comprehension of students.

The ease of use and accessibility of free graphing calculators are transforming math education, equipping students with the tools they need to succeed in the 21st century. It helps students learn by offering them a way to discover and experiment with new formulas or equations.

Graphing Calculator: Key Features and Uses
Feature	Description/Use
Instant Graphing	Visualize equations and functions immediately; see the graphical representation of any equation.
Linear Equations	Graph lines (y = mx + b), explore slopes, and y-intercepts. Easily plot points to see a straight line.
Quadratic Equations	Graph parabolas, find vertices, axis of symmetry, and intercepts.
Trigonometric Functions	Visualize sine and cosine waves, find amplitude, period, and phase shift.
Exponential Functions	Graph exponential functions, identify initial values, and constant ratios.
Logarithmic Functions	Graph logarithmic functions and find their base and intercept points.
Polynomial Functions	Graph cubic and higher-order polynomials, and analyze their roots and properties.
Data Analysis	Create scatter plots, generate trendlines, and analyze data sets.
Equation Solving	Solve equations and inequalities graphically, finding solutions visually.
Vertex Form	Find the equation of a parabola by writing it in vertex form.
Customization	Adjust the graph window, zoom in/out, and customize the appearance of graphs.
Accessibility	Available on the web, making them accessible to students anytime, anywhere.
Problem Solving	Provides visual confirmation of solutions and supports the development of problem-solving skills

To further enhance your understanding of graphing calculators and their functionality, consider exploring the Mathway website. They offer comprehensive resources and examples for various mathematical concepts. Mathway

How to Graph Linear Equations 5 Steps (with Pictures) wikiHow

Details

How To Find The Equation of a Quadratic Function From a Graph YouTube

Details

Details

Detail Author:

Name : Michel Herzog
Username : leatha69
Email : demarco63@jones.net
Birthdate : 1971-08-09
Address : 453 Sandra Shoal Apt. 278 Gradyburgh, IL 91053
Phone : 740-832-9353
Company : Padberg PLC
Job : Aircraft Structure Assemblers
Bio : Praesentium quia reprehenderit non nihil nihil et et. Debitis qui exercitationem et accusantium. Fugiat numquam vitae perferendis temporibus eaque sunt. Illo voluptas ad animi alias voluptatem.

Socials

facebook:

url : https://facebook.com/dschmidt
username : dschmidt
bio : Consequatur qui alias error sed id odio omnis.
followers : 4645
following : 638

twitter:

url : https://twitter.com/dorris_schmidt
username : dorris_schmidt
bio : Excepturi dolores quis maiores nesciunt architecto at. Ea cumque sit eum. Aut autem dolor quo libero repellat nisi. Similique aut et minus tempora quis.
followers : 5465
following : 139