Math Help: Graphing, Equations & More!

23 May, 2025

Are you ready to unlock the secrets of mathematical expression, to visualize the invisible dance of numbers and curves? Mathematics, at its core, is a language, and like any language, it requires both understanding and practice to master, and this article serves as your definitive guide!

Embark on a journey of exploration, where we'll delve into the intricacies of graphing, unraveling the elegant simplicity beneath the seemingly complex equations. We'll learn the step-by-step approach to charting linear equations, discover how to use online tools to our advantage, and apply different techniques to find corresponding values, all without the complexity of complicated formulas. With the aid of our interactive tools, even the most complex equations can be made easily accessible and understood.

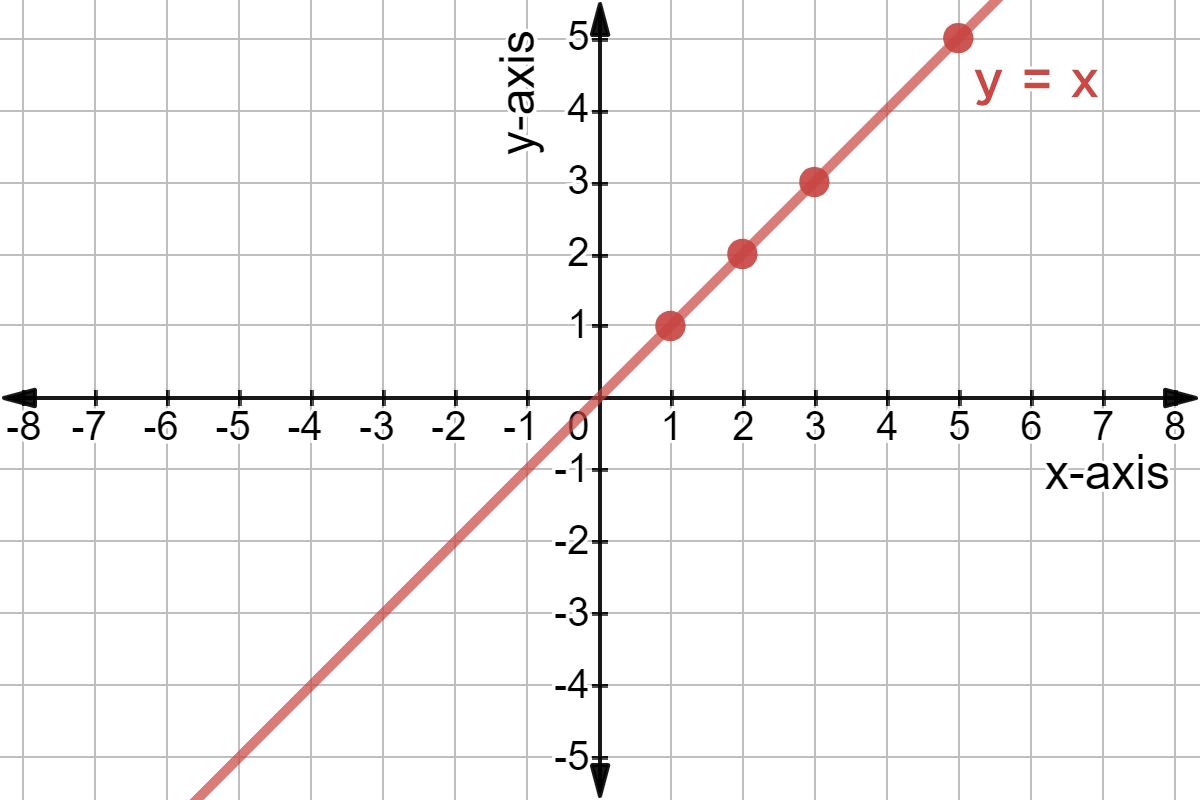
Let's start with the very basics, the foundation upon which all graphing is built. Consider the simple linear equation: y = x. To graph this, we can use the table method. This involves selecting a few values for 'x' and then calculating the corresponding values for 'y'. For example, if x = 0, then y = 0; if x = 1, then y = 1; and if x = -1, then y = -1. Each pair of (x, y) values represents a point on the graph. By plotting these points and connecting them with a straight line, we create the graph of y = x. The graph will display the x and y axis increasing and decreasing in units. It is a straight line which crosses the origin.

Beyond the simple linear equations, there are far more complex forms of expressions that can be graphed. Let's explore other kinds of formulas such as : Y = 3 cos 2x 1, G(x) = log(x) and many more, and even systems of equations. If you have a second equation, just type a semicolon like : y=2x+1 ;

Now, let's delve into the practical tools we can use to graph and visualize these equations. There are online graphing calculators that allow us to input equations and instantly see their graphs. These tools offer numerous features, including the ability to plot points, visualize algebraic equations, add sliders to manipulate variables, and even animate graphs to explore dynamic relationships. You can simply type in your equation, such as y = 2x + 1, and the calculator will generate the graph for you, giving you a complete and instant visual representation.

For those seeking to solve systems of equations, calculators and computer systems offer a particularly useful way. To solve these systems, we can use the substitution method. Enter the system of equations you want to solve for by substitution, and the calculator will do the rest, displaying the solution in both point and equation form. To use the substitution method, isolate one variable from one equation (say 'x'), and substitute its value into the other equation. Then, evaluate the value of the other variable (say 'y') by substituting the equation using algebraic operations. For instance, consider two equations, x + y = 5 and x - y = 1. Solving for x in the first equation gives us x = 5 - y. Substituting this into the second equation, (5 - y) - y = 1, which simplifies to 5 - 2y = 1. Solving for y, we find y = 2. Substituting this value back into either of the original equations, we find x = 3. Therefore, the solution is x = 3, y = 2.

Let's try another example, where understanding the slope is important. Remember the equation, Y = mx + b. Here, 'm' represents the slope, and 'b' represents the y-intercept. To use the slope, we can select two values and plug them into the equation to find the corresponding values, allowing us to plot and visualize the graphs. For example, if the equation is y = 2x + 1, the slope is 2, and the y-intercept is 1. By plugging in different values for x, we can calculate the corresponding y-values.

When exploring equations and graphs, we often encounter parabolas, which are symmetrical, U-shaped curves. To analyze a parabola, you can determine its properties such as the vertex, axis of symmetry, focus, and directrix. To do this, we can use the vertex form, which is . It also provides information that helps us determine the values of 'a', 'h', and 'k', allowing us to understand the parabola's shape, position, and orientation. To get the values for these, it helps to identify and substitute the known values in the formula, and simplify.

Let's consider the equation Y = 3cos(2x) 1. Using the substitution method or utilizing an online graphing tool, we can plot the curve. The graph is a cosine wave, which is vertically scaled by a factor of 3, horizontally compressed by a factor of 2, and shifted downward by 1 unit. This demonstrates how changing the coefficient and constants will affect the overall form of the equation.

When learning this topic, make sure you understand the substitution and table method clearly. In the substitution method, isolate one variable from one equation (say "x"), and its value is substituted into the other equation of the same system. Then evaluate the value of the other variable (say "y") by substituting the equation using algebraic operation. Similarly, in the table method, you select values for x and find the corresponding values for y. Each pair of (x,y) is a point that can be plotted on a graph.

These online tools offer the ability to graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and so much more. These are available for free, instantly graphing your math problems, allowing you to visualize even the most complex math questions.

Mastering graphing isn't just about memorizing formulas or following steps; it's about cultivating a new way of thinking. With our step-by-step guides, the use of different online calculator and all the help, you will be able to understand this topic much better, than you think.

For further learning and information, explore these websites:

Maths is Fun
Khan Academy
GeoGebra

Graphing Linear Functions Examples & Practice Expii

Details

Details

How to Graph the Equation y = 1/x (y equals one over x) YouTube

Details

Detail Author:

Name : Roman Kihn
Username : erdman.luis
Email : larson.madie@gmail.com
Birthdate : 1999-07-05
Address : 778 Haley Junction East Pauline, ND 81801
Phone : +1-952-274-4742
Company : Turner-Wyman
Job : Hunter and Trapper
Bio : Totam est repudiandae molestiae soluta amet rerum. Doloribus dolor dolor minus unde voluptatum consequatur fugit. Et ut rerum voluptatem voluptatem nam.

Socials

twitter:

url : https://twitter.com/predovic2015
username : predovic2015
bio : Quas consequuntur totam pariatur rerum dolorum rerum est. Laboriosam odit culpa ea fuga et non ut. Quibusdam ipsam neque cumque tempore tempore.
followers : 4928
following : 1273

instagram:

url : https://instagram.com/al.predovic
username : al.predovic
bio : Enim occaecati nemo inventore et consequatur fuga. Et quis in cupiditate aut sint quos.
followers : 3112
following : 1931